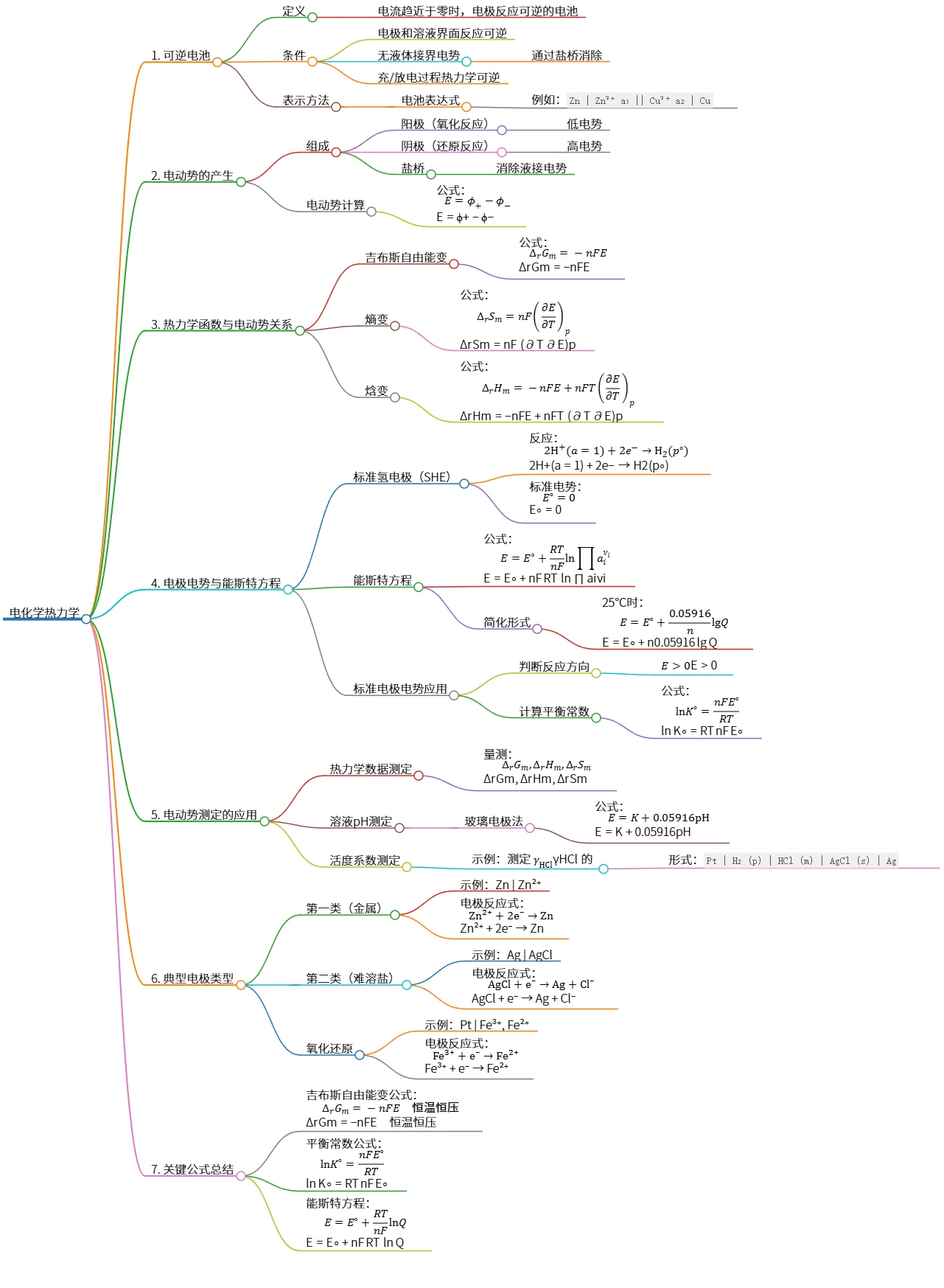
电化学热力学：可逆电池与电动势的关系分析

# 电化学热力学
## 1. 可逆电池
- 定义
  - 电流趋近于零时，电极反应可逆的电池
- 条件
  - 电极和溶液界面反应可逆
  - 无液体接界电势
    - 通过盐桥消除
  - 充/放电过程热力学可逆
- 表示方法
  - 电池表达式
    - 例如：`Zn | Zn²⁺ a₁ || Cu²⁺ a₂ | Cu`
## 2. 电动势的产生
- 组成
  - 阳极（氧化反应）
    - 低电势
  - 阴极（还原反应）
    - 高电势
  - 盐桥
    - 消除液接电势
- 电动势计算
  - 公式：$$E = \phi_+ - \phi_-$$
## 3. 热力学函数与电动势关系
- 吉布斯自由能变
  - 公式：$$\Delta_r G_m = -nFE$$
- 熵变
  - 公式：$$\Delta_r S_m = nF\left(\frac{\partial E}{\partial T}\right)_p$$
- 焓变
  - 公式：$$\Delta_r H_m = -nFE + nFT\left(\frac{\partial E}{\partial T}\right)_p$$
## 4. 电极电势与能斯特方程
- 标准氢电极（SHE）
  - 反应：$$2\text{H}^+ (a=1) + 2e^- \rightarrow \text{H}_2 (p^\circ)$$
  - 标准电势：$$E^\circ=0$$
- 能斯特方程
  - 公式：$$E = E^\circ + \frac{RT}{nF} \ln \prod a_i^{\nu_i}$$
  - 简化形式
    - 25℃时：$$E = E^\circ + \frac{0.05916}{n} \lg Q$$
- 标准电极电势应用
  - 判断反应方向
    - $E > 0$ 自发
  - 计算平衡常数
    - 公式：$$\ln K^\circ = \frac{nFE^\circ}{RT}$$
## 5. 电动势测定的应用
- 热力学数据测定
  - 量测：$$\Delta_r G_m, \Delta_r H_m, \Delta_r S_m$$
- 溶液pH测定
  - 玻璃电极法
    - 公式：$$E = K + 0.05916 \text{pH}$$
- 活度系数测定
  - 示例：测定 $\gamma_{\text{HCl}}$ 的电池
    - 形式：`Pt | H₂ (p) | HCl (m) | AgCl (s) | Ag`
## 6. 典型电极类型
- 第一类（金属）
  - 示例：Zn | Zn²⁺ 
  - 电极反应式：$$\text{Zn²⁺ + 2e⁻ → Zn}$$
- 第二类（难溶盐）
  - 示例：Ag | AgCl 
  - 电极反应式：$$\text{AgCl + e⁻ → Ag + Cl⁻}$$
- 氧化还原
  - 示例：Pt | Fe³⁺, Fe²⁺ 
  - 电极反应式：$$\text{Fe³⁺ + e⁻ → Fe²⁺}$$
## 7. 关键公式总结
- 吉布斯自由能变公式：$$\Delta_r G_m = -nFE \quad \text{恒温恒压}$$
- 平衡常数公式：$$\ln K^\circ = \frac{nFE^\circ}{RT}$$
- 能斯特方程：$$E = E^\circ + \frac{RT}{nF} \ln Q$$