超导电性理论与微观机制研究：从唯象到BCS理论

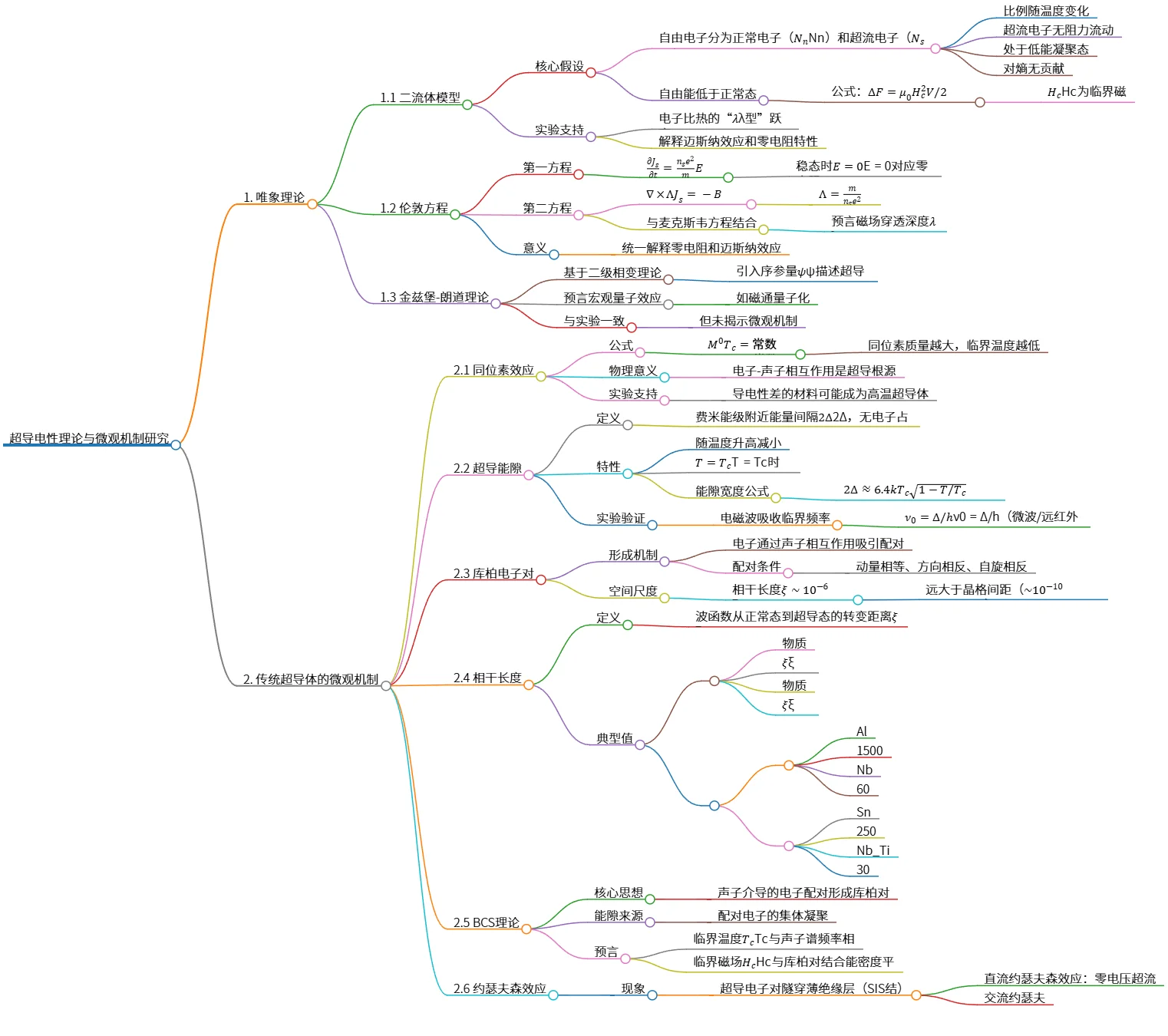
# 超导电性理论与微观机制研究
## 1. 唯象理论
### 1.1 二流体模型
- 核心假设
  - 自由电子分为正常电子（$N_n$）和超流电子（$N_s$）
    - 比例随温度变化
    - 超流电子无阻力流动
    - 处于低能凝聚态
    - 对熵无贡献
  - 自由能低于正常态
    - 公式：$\Delta F = \mu_0 H_c^2 V / 2$ 
      - $H_c$为临界磁场
- 实验支持
  - 电子比热的“$\lambda$型”跃变
  - 解释迈斯纳效应和零电阻特性
### 1.2 伦敦方程
- 第一方程
  - $\frac {\partial J_s} {\partial t} = \frac {n_s e^2}{m} E$
    - 稳态时$E=0$对应零电阻
- 第二方程
  - $\nabla \times \Lambda J_s = -B$ 
    - $\Lambda = \frac {m}{n_s e^2}$
  - 与麦克斯韦方程结合
    - 预言磁场穿透深度$\lambda$
- 意义
  - 统一解释零电阻和迈斯纳效应
### 1.3 金兹堡-朗道理论
- 基于二级相变理论
  - 引入序参量$\psi$描述超导态
- 预言宏观量子效应
  - 如磁通量子化
- 与实验一致
  - 但未揭示微观机制
## 2. 传统超导体的微观机制
### 2.1 同位素效应
- 公式
  - $M^0 T_c = \text{常数}$
    - 同位素质量越大，临界温度越低
- 物理意义
  - 电子-声子相互作用是超导根源
- 实验支持
  - 导电性差的材料可能成为高温超导体
### 2.2 超导能隙
- 定义
  - 费米能级附近能量间隔$2\Delta$，无电子占据
- 特性
  - 随温度升高减小
  - $T=T_c$时$\Delta=0$
  - 能隙宽度公式
    - $2\Delta \approx 6.4 k T_c \sqrt{1-T/T_c}$
- 实验验证
  - 电磁波吸收临界频率
    - $\nu_0 = \Delta / h$（微波/远红外波段）
### 2.3 库柏电子对
- 形成机制
  - 电子通过声子相互作用吸引配对
  - 配对条件
    - 动量相等、方向相反、自旋相反
- 空间尺度
  - 相干长度$\xi \sim 10^{-6}$ m
    - 远大于晶格间距（$\sim 10^{-10}$ m）
### 2.4 相干长度
- 定义
  - 波函数从正常态到超导态的转变距离$\xi$
- 典型值
  | 物质 | $\xi$  nm  | 物质 | $\xi$  nm  |
  |------|------------|------|------------|
  | Al   | 1500       | Nb   | 60         |
  | Sn   | 250        | Nb_Ti| 30         |
### 2.5 BCS理论
- 核心思想
  - 声子介导的电子配对形成库柏对
- 能隙来源
  - 配对电子的集体凝聚
- 预言
  - 临界温度$T_c$与声子谱频率相关
  - 临界磁场$H_c$与库柏对结合能密度平衡
### 2.6 约瑟夫森效应
- 现象
  - 超导电子对隧穿薄绝缘层（SIS结）
    - 直流约瑟夫森效应：零电压超流
    - 交流约瑟夫