勾股定理:从定义到应用的全面解析与历史探讨
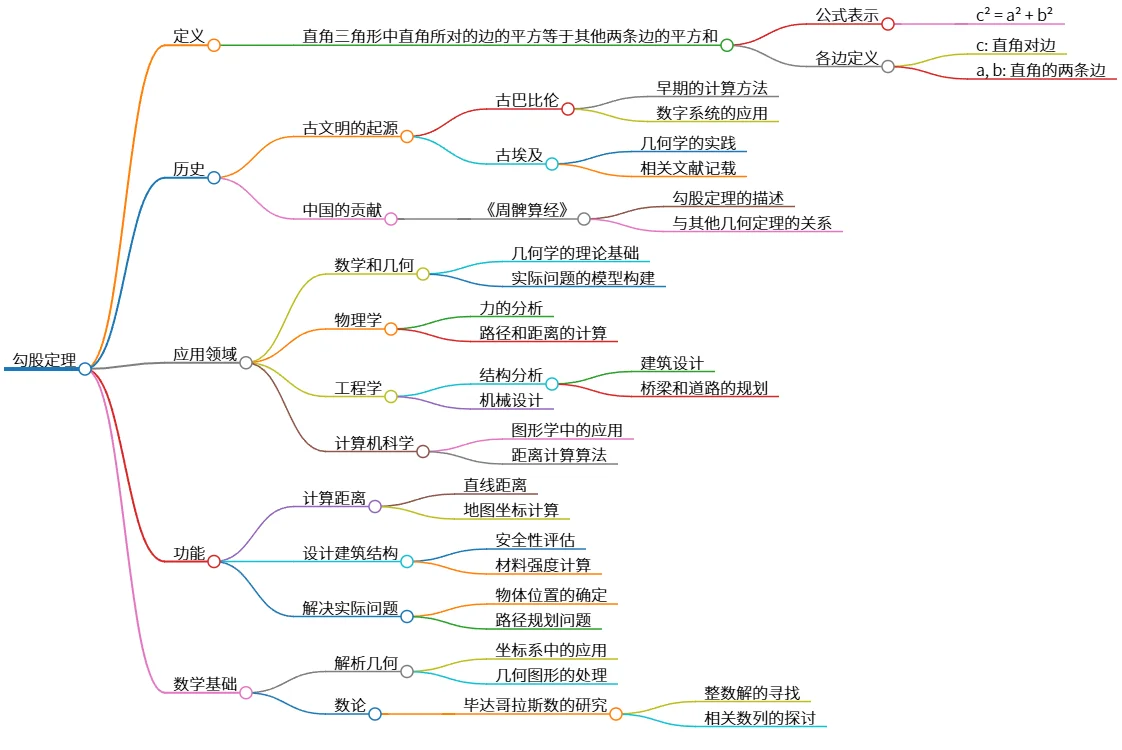
该思维导图旨在阐述勾股定理的相关内容。勾股定理定义为直角三角形中直角对边的平方等于其他两边平方和,公式为c² = a² + b²。其历史可以追溯至古巴比伦和古埃及,并在中国的《周髀算经》中有记载。勾股定理在几何学、物理学、工程学和计算机科学等领域广泛应用,主要功能包括计算距离、设计建筑结构和解决实际问题,并在解析几何和数论中具有重要的数学基础。
源码
# 勾股定理
## 定义
- 直角三角形中直角所对的边的平方等于其他两条边的平方和
- 公式表示
- c² = a² + b²
- 各边定义
- c: 直角对边
- a, b: 直角的两条边
## 历史
- 古文明的起源
- 古巴比伦
- 早期的计算方法
- 数字系统的应用
- 古埃及
- 几何学的实践
- 相关文献记载
- 中国的贡献
- 《周髀算经》
- 勾股定理的描述
- 与其他几何定理的关系
## 应用领域
- 数学和几何
- 几何学的理论基础
- 实际问题的模型构建
- 物理学
- 力的分析
- 路径和距离的计算
- 工程学
- 结构分析
- 建筑设计
- 桥梁和道路的规划
- 机械设计
- 计算机科学
- 图形学中的应用
- 距离计算算法
## 功能
- 计算距离
- 直线距离
- 地图坐标计算
- 设计建筑结构
- 安全性评估
- 材料强度计算
- 解决实际问题
- 物体位置的确定
- 路径规划问题
## 数学基础
- 解析几何
- 坐标系中的应用
- 几何图形的处理
- 数论
- 毕达哥拉斯数的研究
- 整数解的寻找
- 相关数列的探讨
图片