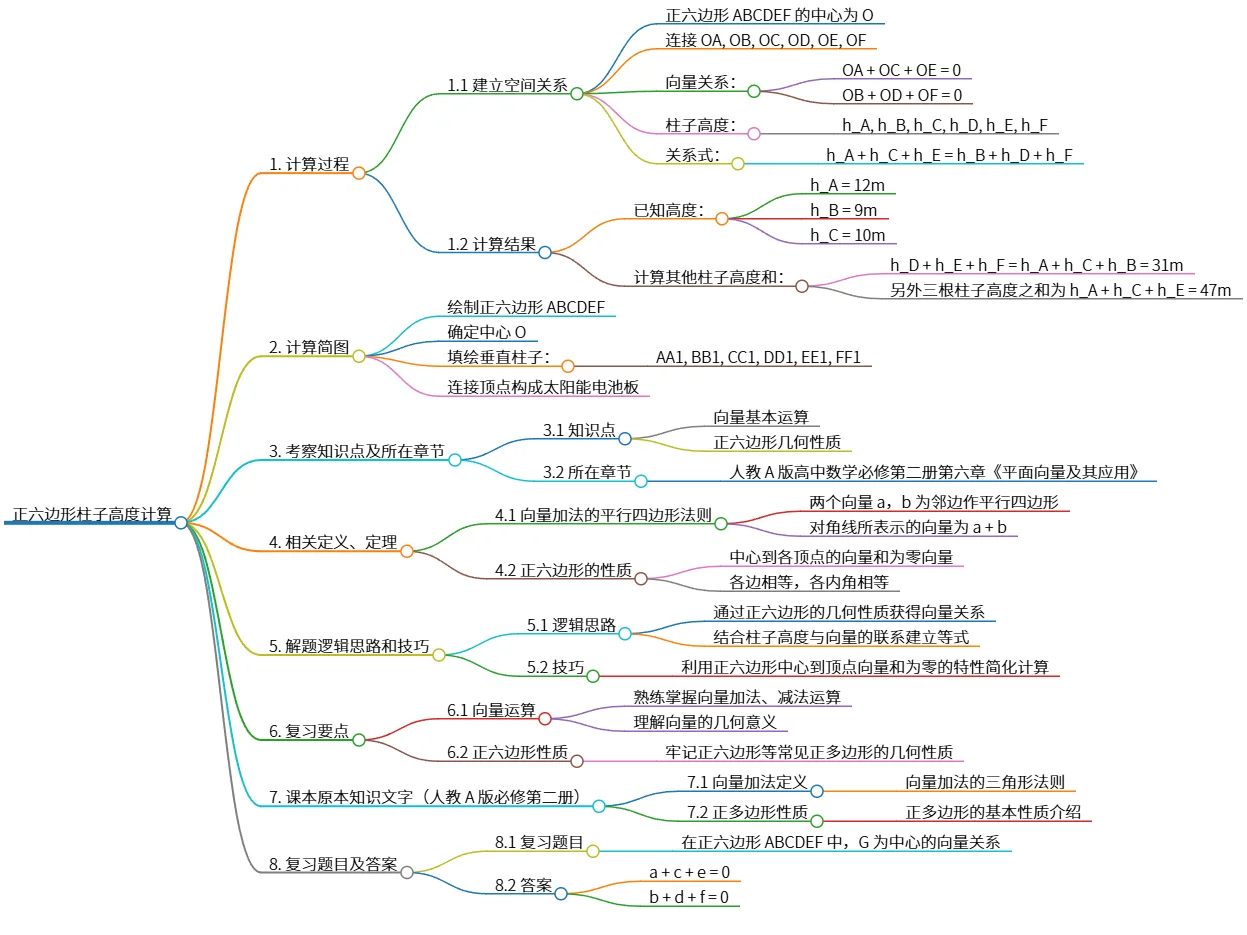
正六边形柱子高度计算方法及其几何性质分析

# 正六边形柱子高度计算
## 1. 计算过程
### 1.1 建立空间关系
- 正六边形 ABCDEF 的中心为 O
- 连接 OA, OB, OC, OD, OE, OF
- 向量关系：
  - OA + OC + OE = 0
  - OB + OD + OF = 0
- 柱子高度：
  - h_A, h_B, h_C, h_D, h_E, h_F
- 关系式：
  - h_A + h_C + h_E = h_B + h_D + h_F
### 1.2 计算结果
- 已知高度：
  - h_A = 12m
  - h_B = 9m
  - h_C = 10m
- 计算其他柱子高度和：
  - h_D + h_E + h_F = h_A + h_C + h_B = 31m
  - 另外三根柱子高度之和为 h_A + h_C + h_E = 47m
## 2. 计算简图
- 绘制正六边形 ABCDEF
- 确定中心 O
- 填绘垂直柱子：
  - AA1, BB1, CC1, DD1, EE1, FF1
- 连接顶点构成太阳能电池板
## 3. 考察知识点及所在章节
### 3.1 知识点
- 向量基本运算
- 正六边形几何性质
### 3.2 所在章节
- 人教 A 版高中数学必修第二册第六章《平面向量及其应用》
## 4. 相关定义、定理
### 4.1 向量加法的平行四边形法则
- 两个向量 a，b 为邻边作平行四边形
- 对角线所表示的向量为 a + b
### 4.2 正六边形的性质
- 中心到各顶点的向量和为零向量
- 各边相等，各内角相等
## 5. 解题逻辑思路和技巧
### 5.1 逻辑思路
- 通过正六边形的几何性质获得向量关系
- 结合柱子高度与向量的联系建立等式
### 5.2 技巧
- 利用正六边形中心到顶点向量和为零的特性简化计算
## 6. 复习要点
### 6.1 向量运算
- 熟练掌握向量加法、减法运算
- 理解向量的几何意义
### 6.2 正六边形性质
- 牢记正六边形等常见正多边形的几何性质
## 7. 课本原本知识文字（人教 A 版必修第二册）
### 7.1 向量加法定义
- 向量加法的三角形法则
### 7.2 正多边形性质
- 正多边形的基本性质介绍
## 8. 复习题目及答案
### 8.1 复习题目
- 在正六边形 ABCDEF 中，G 为中心的向量关系
### 8.2 答案
- a + c + e = 0
- b + d + f = 0