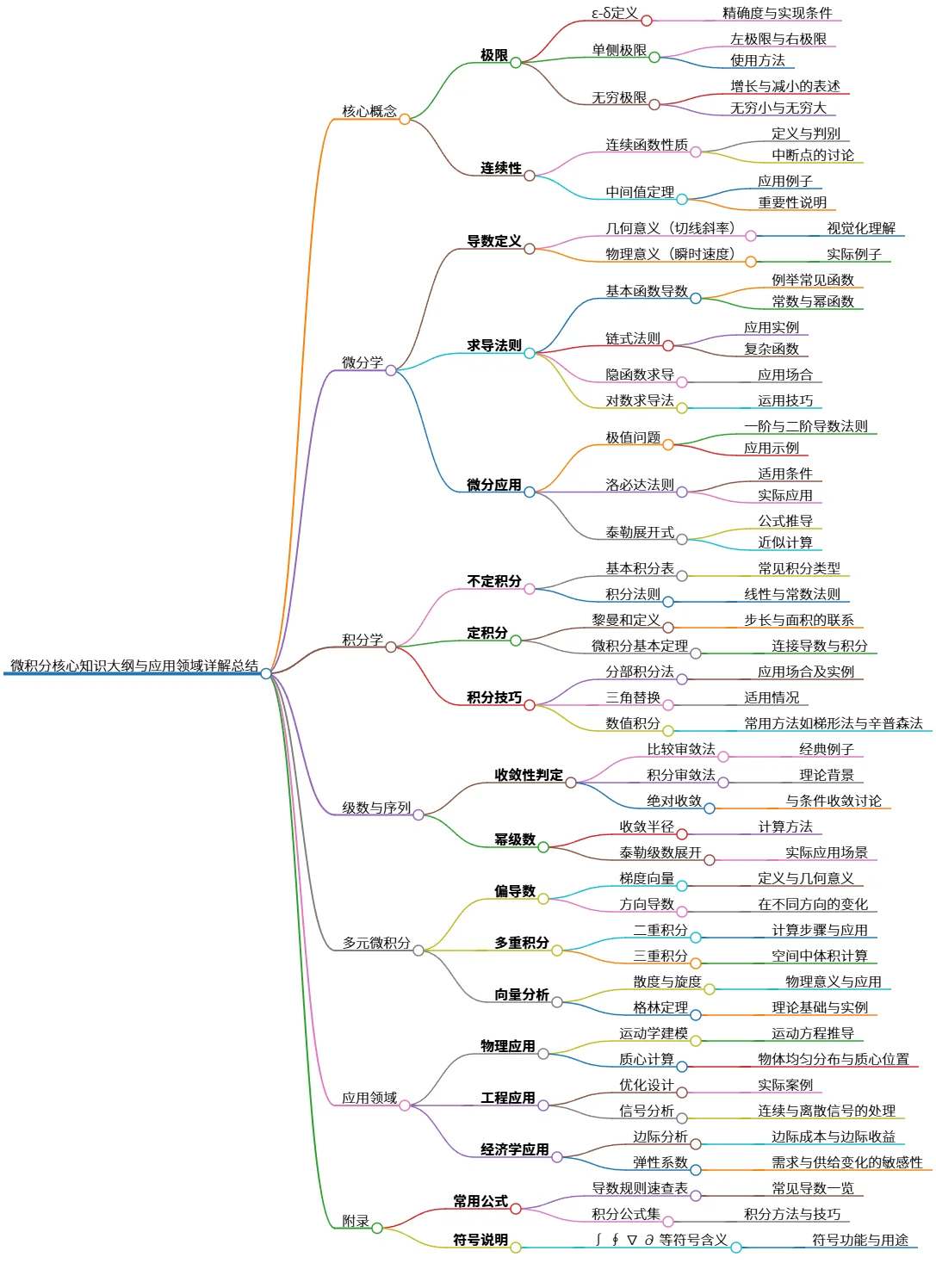
微积分核心知识大纲与应用领域详解总结

# 微积分核心知识大纲与应用领域详解总结
## 核心概念
- **极限**
  - ε-δ定义
    - 精确度与实现条件
  - 单侧极限
    - 左极限与右极限
    - 使用方法
  - 无穷极限
    - 增长与减小的表述
    - 无穷小与无穷大
- **连续性**
  - 连续函数性质
    - 定义与判别
    - 中断点的讨论
  - 中间值定理
    - 应用例子
    - 重要性说明
## 微分学
- **导数定义**
  - 几何意义（切线斜率）
    - 视觉化理解
  - 物理意义（瞬时速度）
    - 实际例子
- **求导法则**
  - 基本函数导数
    - 例举常见函数
    - 常数与幂函数
  - 链式法则
    - 应用实例
    - 复杂函数
  - 隐函数求导
    - 应用场合
  - 对数求导法
    - 运用技巧
- **微分应用**
  - 极值问题
    - 一阶与二阶导数法则
    - 应用示例
  - 洛必达法则
    - 适用条件
    - 实际应用
  - 泰勒展开式
    - 公式推导
    - 近似计算
## 积分学
- **不定积分**
  - 基本积分表
    - 常见积分类型
  - 积分法则
    - 线性与常数法则
- **定积分**
  - 黎曼和定义
    - 步长与面积的联系
  - 微积分基本定理
    - 连接导数与积分
- **积分技巧**
  - 分部积分法
    - 应用场合及实例
  - 三角替换
    - 适用情况
  - 数值积分
    - 常用方法如梯形法与辛普森法
## 级数与序列
- **收敛性判定**
  - 比较审敛法
    - 经典例子
  - 积分审敛法
    - 理论背景
  - 绝对收敛
    - 与条件收敛讨论
- **幂级数**
  - 收敛半径
    - 计算方法
  - 泰勒级数展开
    - 实际应用场景
## 多元微积分
- **偏导数**
  - 梯度向量
    - 定义与几何意义
  - 方向导数
    - 在不同方向的变化
- **多重积分**
  - 二重积分
    - 计算步骤与应用
  - 三重积分
    - 空间中体积计算
- **向量分析**
  - 散度与旋度
    - 物理意义与应用
  - 格林定理
    - 理论基础与实例
## 应用领域
- **物理应用**
  - 运动学建模
    - 运动方程推导
  - 质心计算
    - 物体均匀分布与质心位置
- **工程应用**
  - 优化设计
    - 实际案例
  - 信号分析
    - 连续与离散信号的处理
- **经济学应用**
  - 边际分析
    - 边际成本与边际收益
  - 弹性系数
    - 需求与供给变化的敏感性
## 附录
- **常用公式**
  - 导数规则速查表
    - 常见导数一览
  - 积分公式集
    - 积分方法与技巧
- **符号说明**
  - ∫ ∮ ∇ ∂ 等符号含义
    - 符号功能与用途