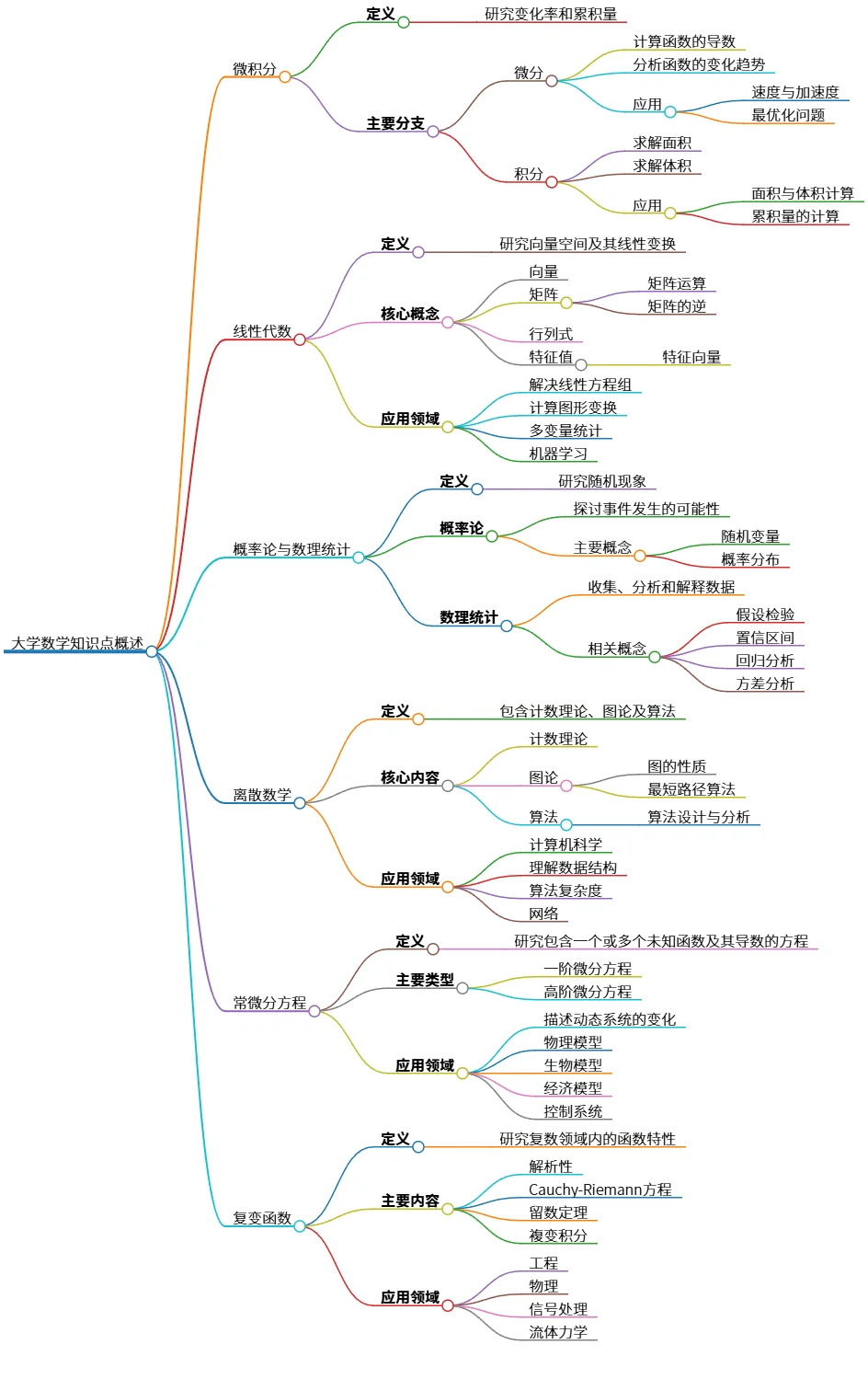
大学数学知识点概述：微积分、线性代数与应用分析

# 大学数学知识点概述
## 微积分
- **定义**
  - 研究变化率和累积量
- **主要分支**
  - 微分
    - 计算函数的导数
    - 分析函数的变化趋势
    - 应用
      - 速度与加速度
      - 最优化问题
  - 积分
    - 求解面积
    - 求解体积
    - 应用
      - 面积与体积计算
      - 累积量的计算
## 线性代数
- **定义**
  - 研究向量空间及其线性变换
- **核心概念**
  - 向量
  - 矩阵
    - 矩阵运算
    - 矩阵的逆
  - 行列式
  - 特征值
    - 特征向量
- **应用领域**
  - 解决线性方程组
  - 计算图形变换
  - 多变量统计
  - 机器学习
## 概率论与数理统计
- **定义**
  - 研究随机现象
- **概率论**
  - 探讨事件发生的可能性
  - 主要概念
    - 随机变量
    - 概率分布
- **数理统计**
  - 收集、分析和解释数据
  - 相关概念
    - 假设检验
    - 置信区间
    - 回归分析
    - 方差分析
## 离散数学
- **定义**
  - 包含计数理论、图论及算法
- **核心内容**
  - 计数理论
  - 图论
    - 图的性质
    - 最短路径算法
  - 算法
    - 算法设计与分析
- **应用领域**
  - 计算机科学
  - 理解数据结构
  - 算法复杂度
  - 网络
## 常微分方程
- **定义**
  - 研究包含一个或多个未知函数及其导数的方程
- **主要类型**
  - 一阶微分方程
  - 高阶微分方程
- **应用领域**
  - 描述动态系统的变化
  - 物理模型
  - 生物模型
  - 经济模型
  - 控制系统
## 复变函数
- **定义**
  - 研究复数领域内的函数特性
- **主要内容**
  - 解析性
  - Cauchy-Riemann方程
  - 留数定理
  - 複变积分
- **应用领域**
  - 工程
  - 物理
  - 信号处理
  - 流体力学