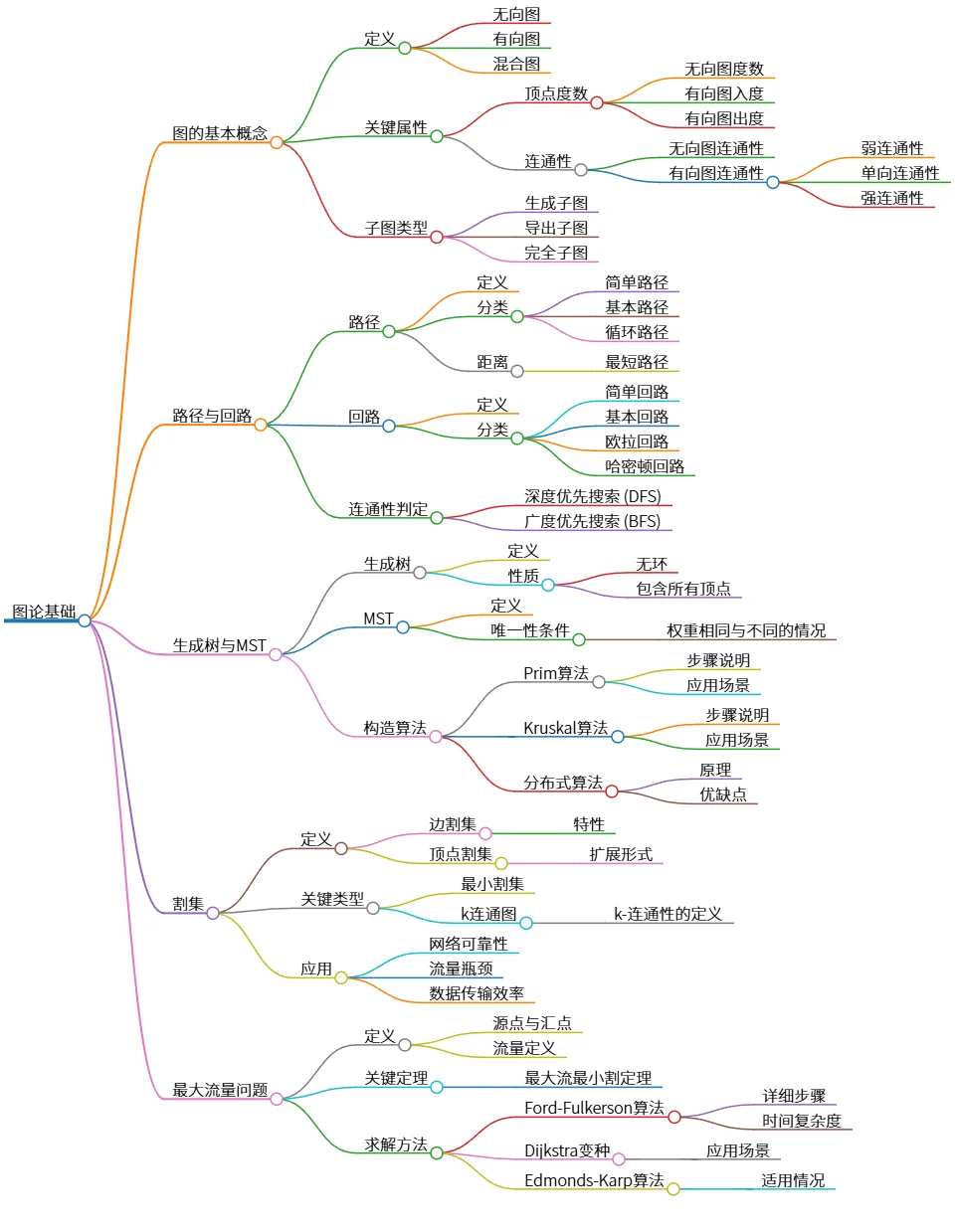
图论基础：路径、生成树、割集与最大流量问题解析

该思维导图概述了图论的基础知识，包括图的基本概念、路径与回路、生成树与最小生成树（MST）、割集以及最大流量问题。内容涵盖了图的分类、关键属性、连通性判定、割集的定义与应用、以及主要算法如Prim、Kruskal和Ford-Fulkerson等。这些知识为理解和解决网络问题奠定了基础。

源码

# 图论基础
## 图的基本概念
### 定义
- 无向图
- 有向图
- 混合图
### 关键属性
- 顶点度数
  - 无向图度数
  - 有向图入度
  - 有向图出度
- 连通性
  - 无向图连通性
  - 有向图连通性
    - 弱连通性
    - 单向连通性
    - 强连通性
### 子图类型
- 生成子图
- 导出子图
- 完全子图
## 路径与回路
### 路径
- 定义
- 分类
  - 简单路径
  - 基本路径
  - 循环路径
- 距离
  - 最短路径 
### 回路
- 定义
- 分类
  - 简单回路
  - 基本回路
  - 欧拉回路
  - 哈密顿回路
### 连通性判定
- 深度优先搜索 (DFS)
- 广度优先搜索 (BFS)
## 生成树与MST
### 生成树
- 定义
- 性质
  - 无环
  - 包含所有顶点
### MST
- 定义
- 唯一性条件
  - 权重相同与不同的情况
### 构造算法
- Prim算法
  - 步骤说明
  - 应用场景
- Kruskal算法
  - 步骤说明
  - 应用场景
- 分布式算法
  - 原理
  - 优缺点
## 割集
### 定义
- 边割集
  - 特性 
- 顶点割集
  - 扩展形式
### 关键类型
- 最小割集
- k连通图
  - k-连通性的定义
### 应用
- 网络可靠性
- 流量瓶颈
- 数据传输效率
## 最大流量问题
### 定义
- 源点与汇点
- 流量定义
### 关键定理
- 最大流最小割定理
### 求解方法
- Ford-Fulkerson算法
  - 详细步骤
  - 时间复杂度
- Dijkstra变种
  - 应用场景
- Edmonds-Karp算法
  - 适用情况

图片