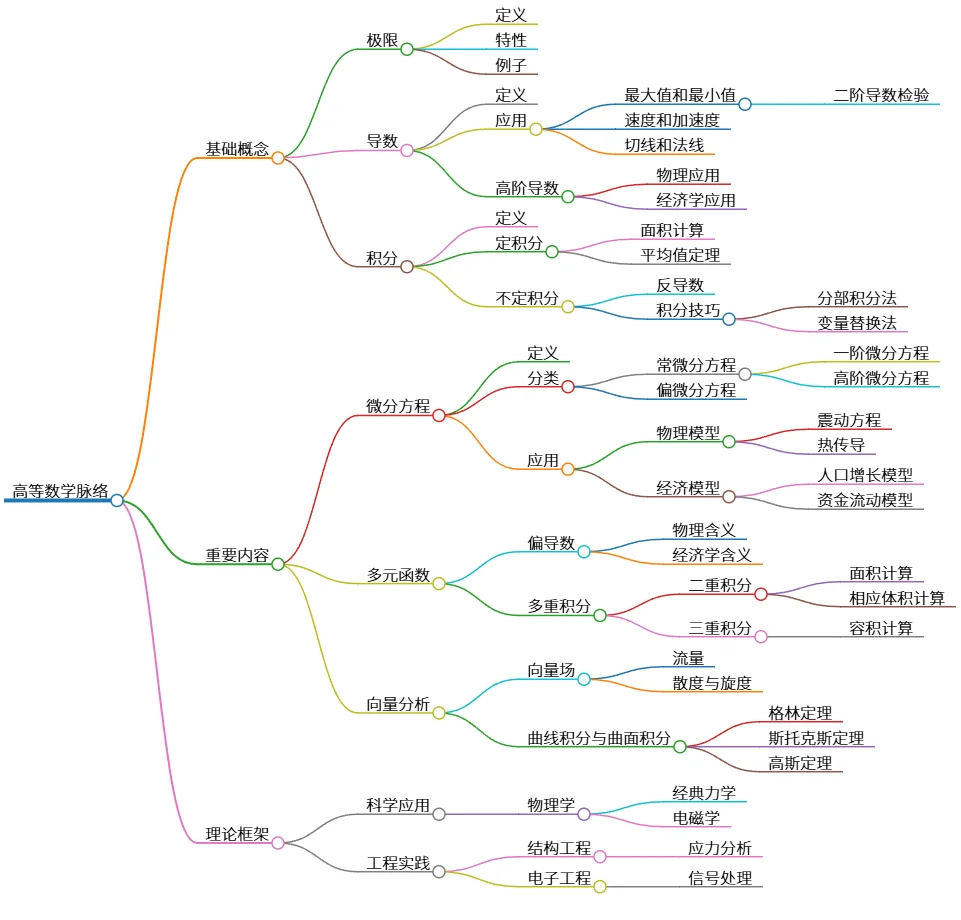
高等数学脉络:基础概念、重要内容与理论框架
该思维导图展示了高等数学的脉络,包括基础概念如极限、导数和积分,每个概念下细分其定义、特性及应用。此外,重要内容涵盖微分方程、多元函数及向量分析,探讨其在物理和经济模型中的应用。最后,理论框架部分强调其在科学应用和工程实践中的重要性,以此提供高等数学的全面视角。
源码
# 高等数学脉络
## 基础概念
### 极限
#### 定义
#### 特性
#### 例子
### 导数
#### 定义
#### 应用
##### 最大值和最小值
###### 二阶导数检验
##### 速度和加速度
##### 切线和法线
#### 高阶导数
##### 物理应用
##### 经济学应用
### 积分
#### 定义
#### 定积分
##### 面积计算
##### 平均值定理
#### 不定积分
##### 反导数
##### 积分技巧
###### 分部积分法
###### 变量替换法
## 重要内容
### 微分方程
#### 定义
#### 分类
##### 常微分方程
###### 一阶微分方程
###### 高阶微分方程
##### 偏微分方程
#### 应用
##### 物理模型
###### 震动方程
###### 热传导
##### 经济模型
###### 人口增长模型
###### 资金流动模型
### 多元函数
#### 偏导数
##### 物理含义
##### 经济学含义
#### 多重积分
##### 二重积分
###### 面积计算
###### 相应体积计算
##### 三重积分
###### 容积计算
### 向量分析
#### 向量场
##### 流量
##### 散度与旋度
#### 曲线积分与曲面积分
##### 格林定理
##### 斯托克斯定理
##### 高斯定理
## 理论框架
### 科学应用
#### 物理学
##### 经典力学
##### 电磁学
### 工程实践
#### 结构工程
##### 应力分析
#### 电子工程
##### 信号处理
图片