定积分及其在物理与经济学中的应用探讨
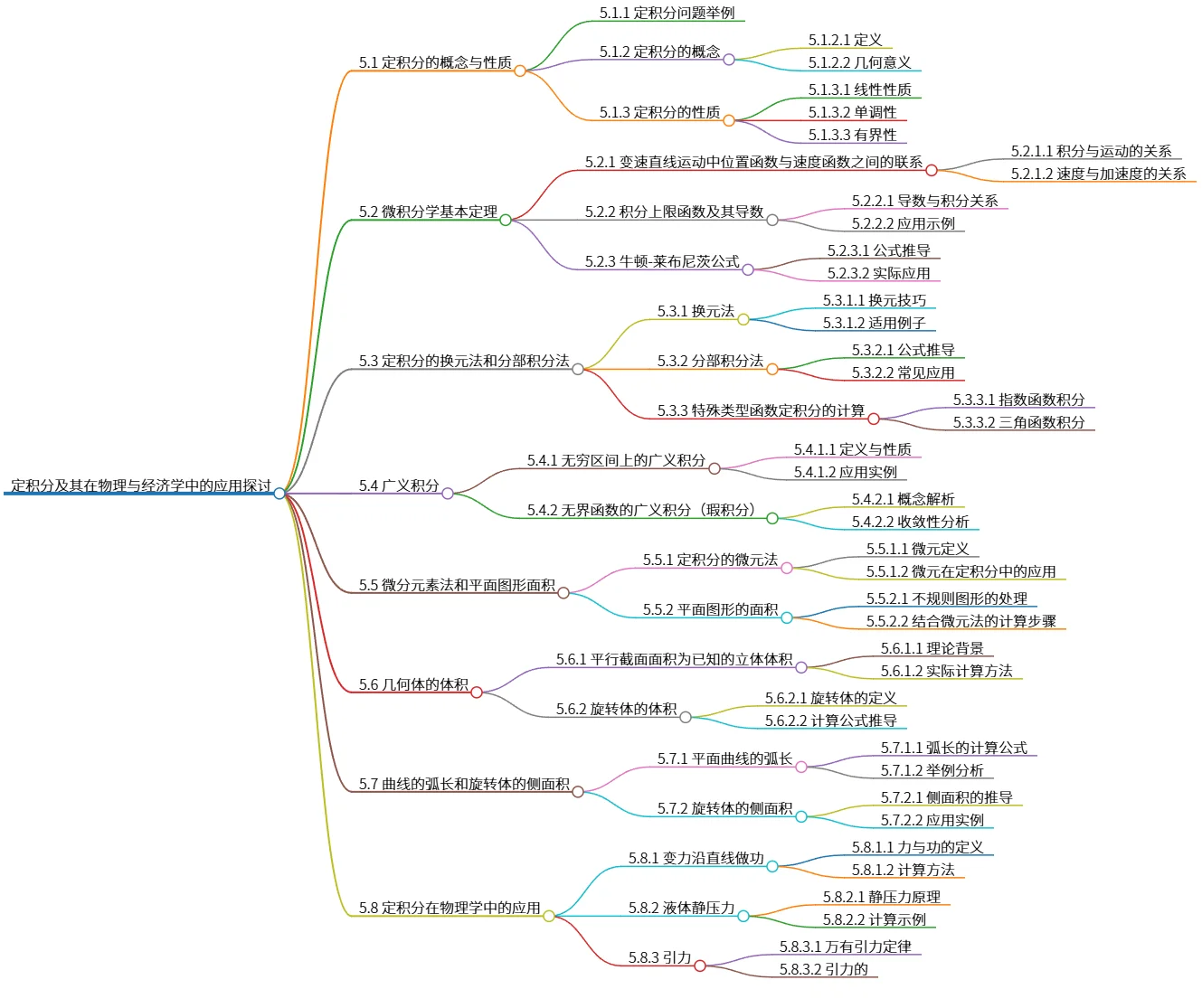
该思维导图概述了第5章定积分及其应用的主要内容,包括定积分的概念、性质以及基本定理。讨论了定积分的换元法和分部积分法、广义积分、微分元素法在平面图形面积和几何体体积计算中的应用。此外,介绍了曲线的弧长及旋转体的侧面积,最后探讨了定积分在物理和经济学中的具体应用,如变力做功和最大利润问题。
源码
# 定积分及其在物理与经济学中的应用探讨
## 5.1 定积分的概念与性质
### 5.1.1 定积分问题举例
### 5.1.2 定积分的概念
#### 5.1.2.1 定义
#### 5.1.2.2 几何意义
### 5.1.3 定积分的性质
#### 5.1.3.1 线性性质
#### 5.1.3.2 单调性
#### 5.1.3.3 有界性
## 5.2 微积分学基本定理
### 5.2.1 变速直线运动中位置函数与速度函数之间的联系
#### 5.2.1.1 积分与运动的关系
#### 5.2.1.2 速度与加速度的关系
### 5.2.2 积分上限函数及其导数
#### 5.2.2.1 导数与积分关系
#### 5.2.2.2 应用示例
### 5.2.3 牛顿-莱布尼茨公式
#### 5.2.3.1 公式推导
#### 5.2.3.2 实际应用
## 5.3 定积分的换元法和分部积分法
### 5.3.1 换元法
#### 5.3.1.1 换元技巧
#### 5.3.1.2 适用例子
### 5.3.2 分部积分法
#### 5.3.2.1 公式推导
#### 5.3.2.2 常见应用
### 5.3.3 特殊类型函数定积分的计算
#### 5.3.3.1 指数函数积分
#### 5.3.3.2 三角函数积分
## 5.4 广义积分
### 5.4.1 无穷区间上的广义积分
#### 5.4.1.1 定义与性质
#### 5.4.1.2 应用实例
### 5.4.2 无界函数的广义积分(瑕积分)
#### 5.4.2.1 概念解析
#### 5.4.2.2 收敛性分析
## 5.5 微分元素法和平面图形面积
### 5.5.1 定积分的微元法
#### 5.5.1.1 微元定义
#### 5.5.1.2 微元在定积分中的应用
### 5.5.2 平面图形的面积
#### 5.5.2.1 不规则图形的处理
#### 5.5.2.2 结合微元法的计算步骤
## 5.6 几何体的体积
### 5.6.1 平行截面面积为已知的立体体积
#### 5.6.1.1 理论背景
#### 5.6.1.2 实际计算方法
### 5.6.2 旋转体的体积
#### 5.6.2.1 旋转体的定义
#### 5.6.2.2 计算公式推导
## 5.7 曲线的弧长和旋转体的侧面积
### 5.7.1 平面曲线的弧长
#### 5.7.1.1 弧长的计算公式
#### 5.7.1.2 举例分析
### 5.7.2 旋转体的侧面积
#### 5.7.2.1 侧面积的推导
#### 5.7.2.2 应用实例
## 5.8 定积分在物理学中的应用
### 5.8.1 变力沿直线做功
#### 5.8.1.1 力与功的定义
#### 5.8.1.2 计算方法
### 5.8.2 液体静压力
#### 5.8.2.1 静压力原理
#### 5.8.2.2 计算示例
### 5.8.3 引力
#### 5.8.3.1 万有引力定律
#### 5.8.3.2 引力的
图片