导数、微分及其计算与几何意义探讨
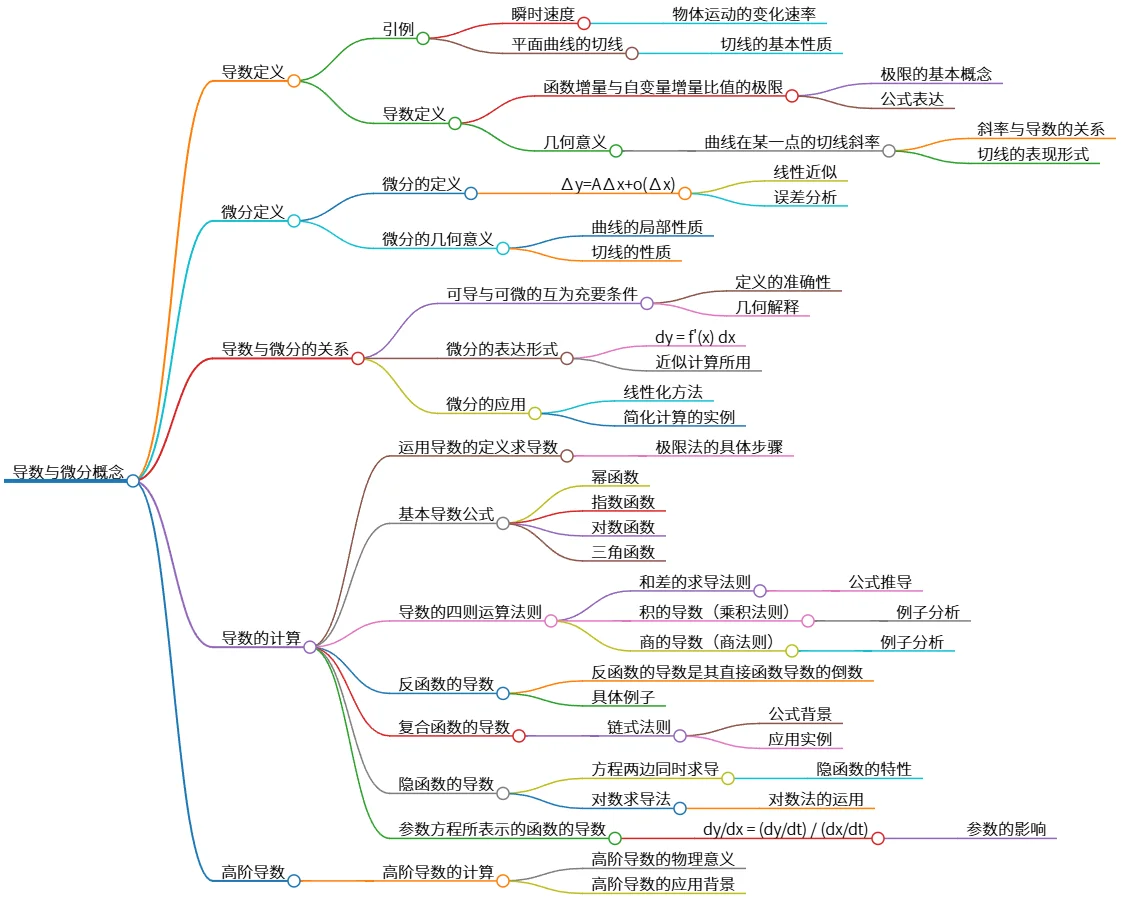
该思维导图介绍了导数与微分的基本概念及其关系,包括导数的定义、几何意义,以及微分的定义和几何意义。文中探讨了导数的计算方法,如导数的定义求导、基本导数公式及其运算法则,包括和差法则、积法则、商法则、反函数和复合函数的导数等。同时,讨论了隐函数及参数方程的导数,并介绍了高阶导数的计算。
源码
# 导数与微分概念
## 导数定义
### 引例
#### 瞬时速度
##### 物体运动的变化速率
#### 平面曲线的切线
##### 切线的基本性质
### 导数定义
#### 函数增量与自变量增量比值的极限
##### 极限的基本概念
##### 公式表达
#### 几何意义
##### 曲线在某一点的切线斜率
###### 斜率与导数的关系
###### 切线的表现形式
## 微分定义
### 微分的定义
#### ∆y=A∆x+ο(∆x)
##### 线性近似
##### 误差分析
### 微分的几何意义
#### 曲线的局部性质
#### 切线的性质
## 导数与微分的关系
### 可导与可微的互为充要条件
#### 定义的准确性
#### 几何解释
### 微分的表达形式
#### dy = f'(x) dx
#### 近似计算所用
### 微分的应用
#### 线性化方法
#### 简化计算的实例
## 导数的计算
### 运用导数的定义求导数
#### 极限法的具体步骤
### 基本导数公式
#### 幂函数
#### 指数函数
#### 对数函数
#### 三角函数
### 导数的四则运算法则
#### 和差的求导法则
##### 公式推导
#### 积的导数(乘积法则)
##### 例子分析
#### 商的导数(商法则)
##### 例子分析
### 反函数的导数
#### 反函数的导数是其直接函数导数的倒数
#### 具体例子
### 复合函数的导数
#### 链式法则
##### 公式背景
##### 应用实例
### 隐函数的导数
#### 方程两边同时求导
##### 隐函数的特性
#### 对数求导法
##### 对数法的运用
### 参数方程所表示的函数的导数
#### dy/dx = (dy/dt) / (dx/dt)
##### 参数的影响
## 高阶导数
### 高阶导数的计算
#### 高阶导数的物理意义
#### 高阶导数的应用背景
图片