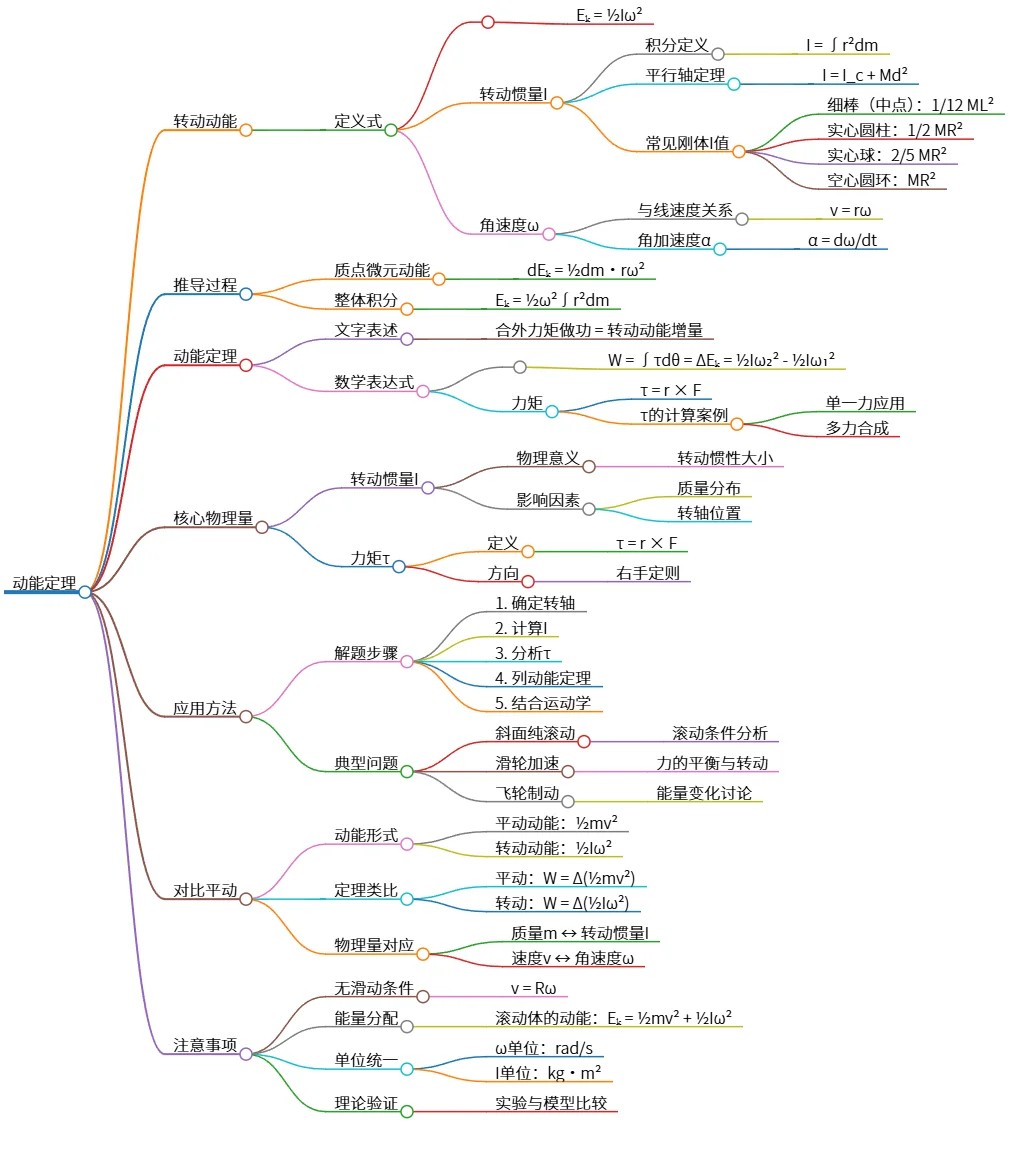
动能定理与转动动能的公式、推导和应用

该思维导图总结了动能定理及转动动能的相关知识。转动动能由公式Eₖ=½Iω²定义，其中转动惯量I与物体的质量分布和转轴位置有关。动能定理表明合外力矩做功等于转动动能增量，推导过程中涉及质点微元动能和整体积分。应用方法包括确定转轴、计算I、分析力矩等步骤，同时对比了平动和转动的动能形式与定理类比。注意事项涵盖无滑动条件和能量分配问题。

源码

# 动能定理
## 转动动能
### 定义式
- Eₖ = ½Iω²
#### 转动惯量I
- 积分定义
  - I = ∫r²dm
- 平行轴定理
  - I = I_c + Md²
- 常见刚体I值
  - 细棒（中点）：1/12 ML²
  - 实心圆柱：1/2 MR²
  - 实心球：2/5 MR²
  - 空心圆环：MR²
#### 角速度ω
- 与线速度关系
  - v = rω
- 角加速度α
  - α = dω/dt

## 推导过程
### 质点微元动能
- dEₖ = ½dm·rω²
### 整体积分
- Eₖ = ½ω²∫r²dm

## 动能定理
### 文字表述
- 合外力矩做功 = 转动动能增量
### 数学表达式
- W = ∫τdθ = ΔEₖ = ½Iω₂² - ½Iω₁²
#### 力矩
- τ = r × F
- τ的计算案例
  - 单一力应用
  - 多力合成

## 核心物理量
### 转动惯量I
- 物理意义
  - 转动惯性大小
- 影响因素
  - 质量分布
  - 转轴位置
### 力矩τ
- 定义
  - τ = r × F
- 方向
  - 右手定则

## 应用方法
### 解题步骤
1. 确定转轴
2. 计算I
3. 分析τ
4. 列动能定理
5. 结合运动学
### 典型问题
- 斜面纯滚动
  - 滚动条件分析
- 滑轮加速
  - 力的平衡与转动
- 飞轮制动
  - 能量变化讨论

## 对比平动
### 动能形式
- 平动动能：½mv²
- 转动动能：½Iω²
### 定理类比
- 平动：W = Δ(½mv²)
- 转动：W = Δ(½Iω²)
### 物理量对应
- 质量m ↔ 转动惯量I
- 速度v ↔ 角速度ω

## 注意事项
### 无滑动条件
- v = Rω
### 能量分配
- 滚动体的动能：Eₖ = ½mv² + ½Iω²
### 单位统一
- ω单位：rad/s
- I单位：kg·m²
### 理论验证
- 实验与模型比较

图片