常微分方程知识框架与解法概述
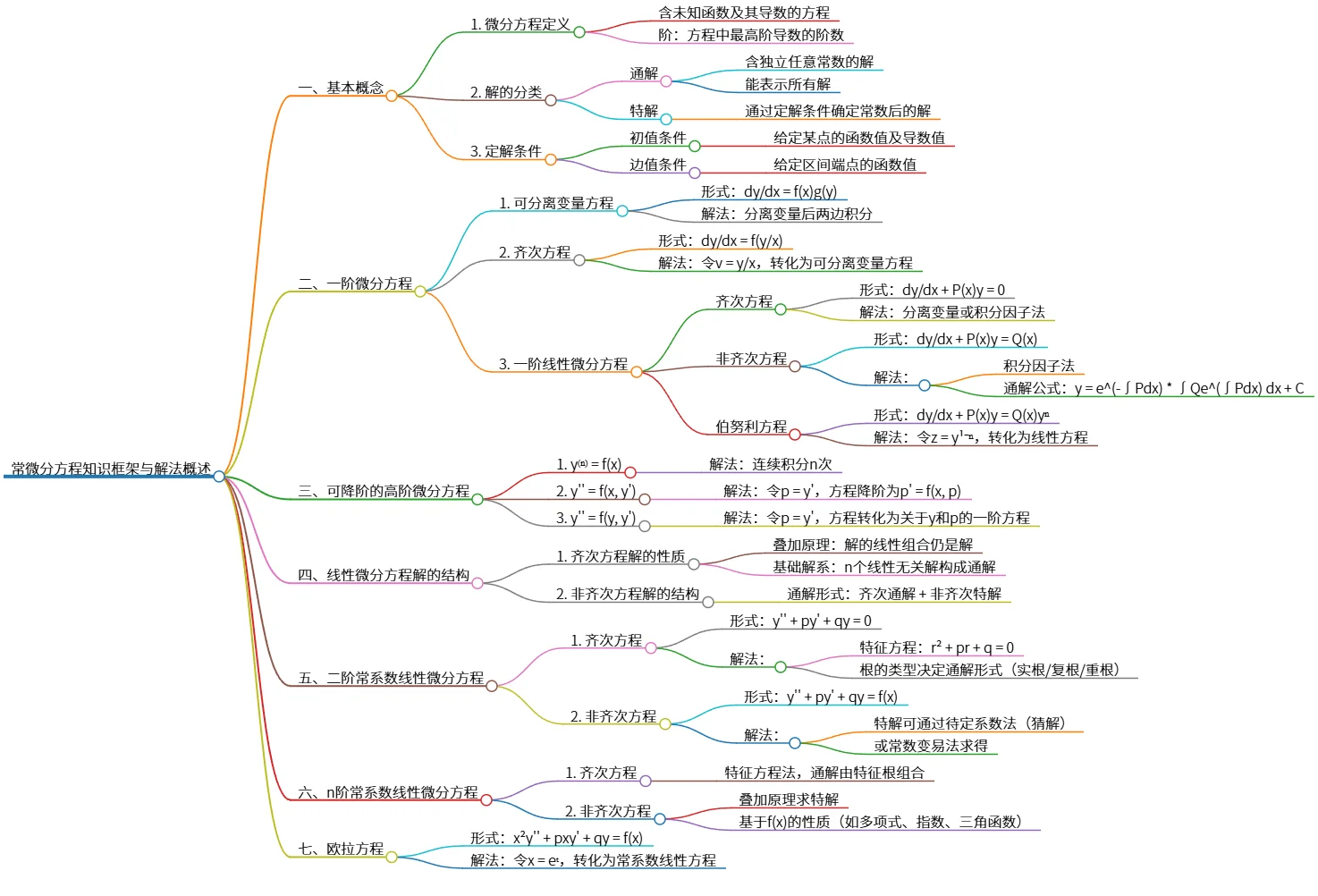
该思维导图概述了常微分方程的基本概念、分类、定解条件以及一阶和高阶微分方程的解法,包括可分离变量方程、线性微分方程和可降阶方程的处理方法。还讨论了线性微分方程解的结构、二阶常系数线性微分方程的特征方程法及求解技巧,最后介绍了欧拉方程的转化解法,全面展示了常微分方程的知识框架。
源码
# 常微分方程知识框架与解法概述
## 一、基本概念
### 1. 微分方程定义
- 含未知函数及其导数的方程
- 阶:方程中最高阶导数的阶数
### 2. 解的分类
#### 通解
- 含独立任意常数的解
- 能表示所有解
#### 特解
- 通过定解条件确定常数后的解
### 3. 定解条件
#### 初值条件
- 给定某点的函数值及导数值
#### 边值条件
- 给定区间端点的函数值
## 二、一阶微分方程
### 1. 可分离变量方程
- 形式:dy/dx = f(x)g(y)
- 解法:分离变量后两边积分
### 2. 齐次方程
- 形式:dy/dx = f(y/x)
- 解法:令v = y/x,转化为可分离变量方程
### 3. 一阶线性微分方程
#### 齐次方程
- 形式:dy/dx + P(x)y = 0
- 解法:分离变量或积分因子法
#### 非齐次方程
- 形式:dy/dx + P(x)y = Q(x)
- 解法:
- 积分因子法
- 通解公式:y = e^(-∫Pdx) * ∫Qe^(∫Pdx) dx + C
#### 伯努利方程
- 形式:dy/dx + P(x)y = Q(x)yⁿ
- 解法:令z = y¹⁻ⁿ,转化为线性方程
## 三、可降阶的高阶微分方程
### 1. y⁽ⁿ⁾ = f(x)
- 解法:连续积分n次
### 2. y'' = f(x, y')
- 解法:令p = y',方程降阶为p' = f(x, p)
### 3. y'' = f(y, y')
- 解法:令p = y',方程转化为关于y和p的一阶方程
## 四、线性微分方程解的结构
### 1. 齐次方程解的性质
- 叠加原理:解的线性组合仍是解
- 基础解系:n个线性无关解构成通解
### 2. 非齐次方程解的结构
- 通解形式:齐次通解 + 非齐次特解
## 五、二阶常系数线性微分方程
### 1. 齐次方程
- 形式:y'' + py' + qy = 0
- 解法:
- 特征方程:r² + pr + q = 0
- 根的类型决定通解形式(实根/复根/重根)
### 2. 非齐次方程
- 形式:y'' + py' + qy = f(x)
- 解法:
- 特解可通过待定系数法(猜解)
- 或常数变易法求得
## 六、n阶常系数线性微分方程
### 1. 齐次方程
- 特征方程法,通解由特征根组合
### 2. 非齐次方程
- 叠加原理求特解
- 基于f(x)的性质(如多项式、指数、三角函数)
## 七、欧拉方程
- 形式:x²y'' + pxy' + qy = f(x)
- 解法:令x = eᵗ,转化为常系数线性方程
图片