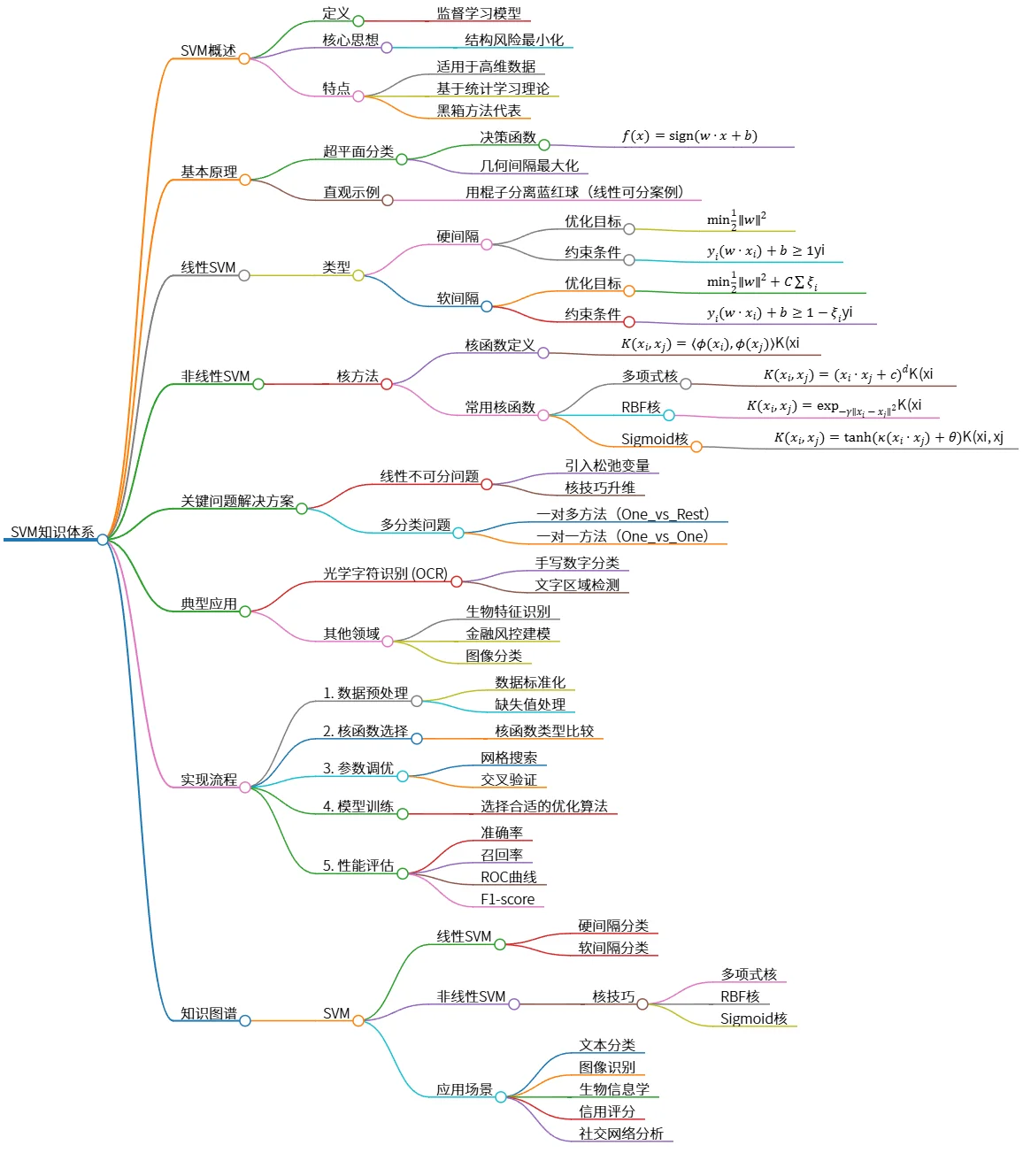
SVM知识体系：概述、原理、应用与实现流程解析

该思维导图概述了支持向量机（SVM）的知识体系，包括定义、核心思想和特点。内容涵盖基本原理、线性与非线性SVM、关键问题解决方案（如线性不可分与多分类问题），以及典型应用（如光学字符识别和生物特征识别）。此外，展示了实现流程，包括数据预处理、核函数选择和模型评估，最后列出了相关知识图谱，涉及线性与非线性SVM的分类方式和应用场景。

源码

# SVM知识体系
## SVM概述
- 定义
  - 监督学习模型
- 核心思想
  - 结构风险最小化
- 特点
  - 适用于高维数据
  - 基于统计学习理论
  - 黑箱方法代表
## 基本原理
- 超平面分类
  - 决策函数
    - $f(x) = \text{sign}(w \cdot x + b)$
  - 几何间隔最大化
- 直观示例
  - 用棍子分离蓝红球（线性可分案例）
## 线性SVM
- 类型
  - 硬间隔
    - 优化目标
      - $\min \frac{1}{2} \|w\|^2$
    - 约束条件
      - $y_i (w \cdot x_i) + b \geq 1$
  - 软间隔
    - 优化目标
      - $\min \frac{1}{2} \|w\|^2 + C \sum \xi_i$
    - 约束条件
      - $y_i (w \cdot x_i) + b \geq 1 - \xi_i$
## 非线性SVM
- 核方法
  - 核函数定义
    - $K(x_i, x_j) = \langle \phi(x_i), \phi(x_j) \rangle$
  - 常用核函数
    - 多项式核
      - $K(x_i, x_j) = (x_i \cdot x_j + c)^d$
    - RBF核
      - $K(x_i, x_j) = \exp_{-\gamma \|x_i - x_j\|^2}$
    - Sigmoid核
      - $K(x_i, x_j) = \tanh(\kappa (x_i \cdot x_j) + \theta)$
## 关键问题解决方案
- 线性不可分问题
  - 引入松弛变量
  - 核技巧升维
- 多分类问题
  - 一对多方法（One_vs_Rest）
  - 一对一方法（One_vs_One）
## 典型应用
- 光学字符识别 (OCR)
  - 手写数字分类
  - 文字区域检测
- 其他领域
  - 生物特征识别
  - 金融风控建模
  - 图像分类
## 实现流程
1. 数据预处理
   - 数据标准化
   - 缺失值处理
2. 核函数选择
   - 核函数类型比较
3. 参数调优
   - 网格搜索
   - 交叉验证
4. 模型训练
   - 选择合适的优化算法
5. 性能评估
   - 准确率
   - 召回率
   - ROC曲线
   - F1-score
## 知识图谱
- SVM
  - 线性SVM
    - 硬间隔分类
    - 软间隔分类
  - 非线性SVM
    - 核技巧
      - 多项式核
      - RBF核
      - Sigmoid核
  - 应用场景
    - 文本分类
    - 图像识别
    - 生物信息学
    - 信用评分
    - 社交网络分析

图片