第二章 线性表的定义、特点及基本操作实现
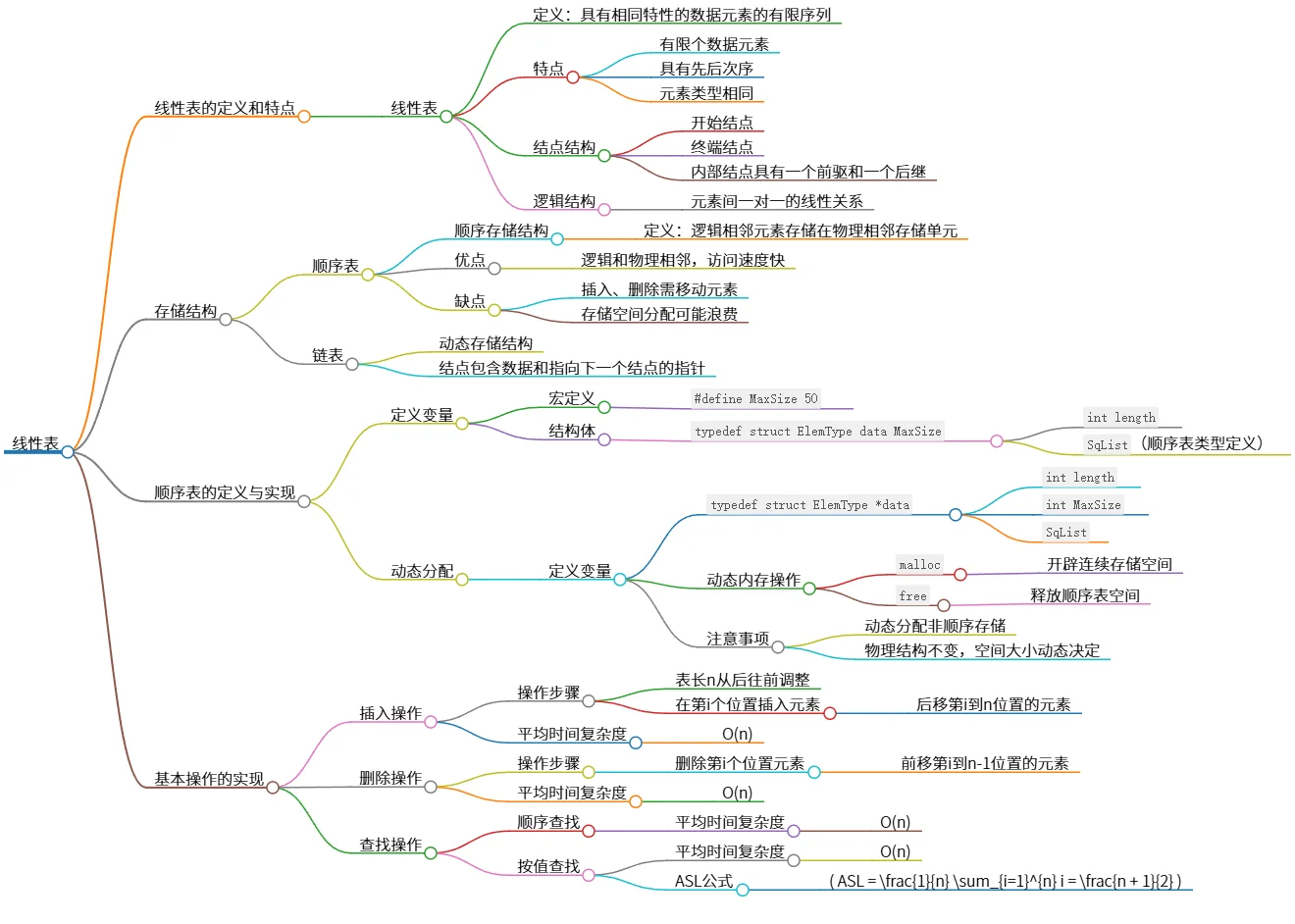
该思维导图介绍了线性表的定义、特点及存储结构,包括顺序表和链表。顺序存储结构将逻辑相邻的数据元素存于物理相邻的存储单元,具有优缺点,同时展示了动态分配和基本操作的实现,包含插入、删除和查找的平均时间复杂度。插入和删除操作需移动大量元素,查找操作采用顺序查找,平均时间复杂度均为O(n)。
源码
# 线性表
## 线性表的定义和特点
- 线性表
- 定义:具有相同特性的数据元素的有限序列
- 特点
- 有限个数据元素
- 具有先后次序
- 元素类型相同
- 结点结构
- 开始结点
- 终端结点
- 内部结点具有一个前驱和一个后继
- 逻辑结构
- 元素间一对一的线性关系
## 存储结构
- 顺序表
- 顺序存储结构
- 定义:逻辑相邻元素存储在物理相邻存储单元
- 优点
- 逻辑和物理相邻,访问速度快
- 缺点
- 插入、删除需移动元素
- 存储空间分配可能浪费
- 链表
- 动态存储结构
- 结点包含数据和指向下一个结点的指针
## 顺序表的定义与实现
### 定义变量
- 宏定义
- `#define MaxSize 50`
- 结构体
- `typedef struct ElemType data MaxSize`
- `int length`
- `SqList`(顺序表类型定义)
### 动态分配
- 定义变量
- `typedef struct ElemType *data`
- `int length`
- `int MaxSize`
- `SqList`
- 动态内存操作
- `malloc`
- 开辟连续存储空间
- `free`
- 释放顺序表空间
- 注意事项
- 动态分配非顺序存储
- 物理结构不变,空间大小动态决定
## 基本操作的实现
### 插入操作
- 操作步骤
- 表长n从后往前调整
- 在第i个位置插入元素
- 后移第i到n位置的元素
- 平均时间复杂度
- O(n)
### 删除操作
- 操作步骤
- 删除第i个位置元素
- 前移第i到n-1位置的元素
- 平均时间复杂度
- O(n)
### 查找操作
- 顺序查找
- 平均时间复杂度
- O(n)
- 按值查找
- 平均时间复杂度
- O(n)
- ASL公式
- \( ASL = \frac{1}{n} \sum_{i=1}^{n} i = \frac{n + 1}{2} \)
图片