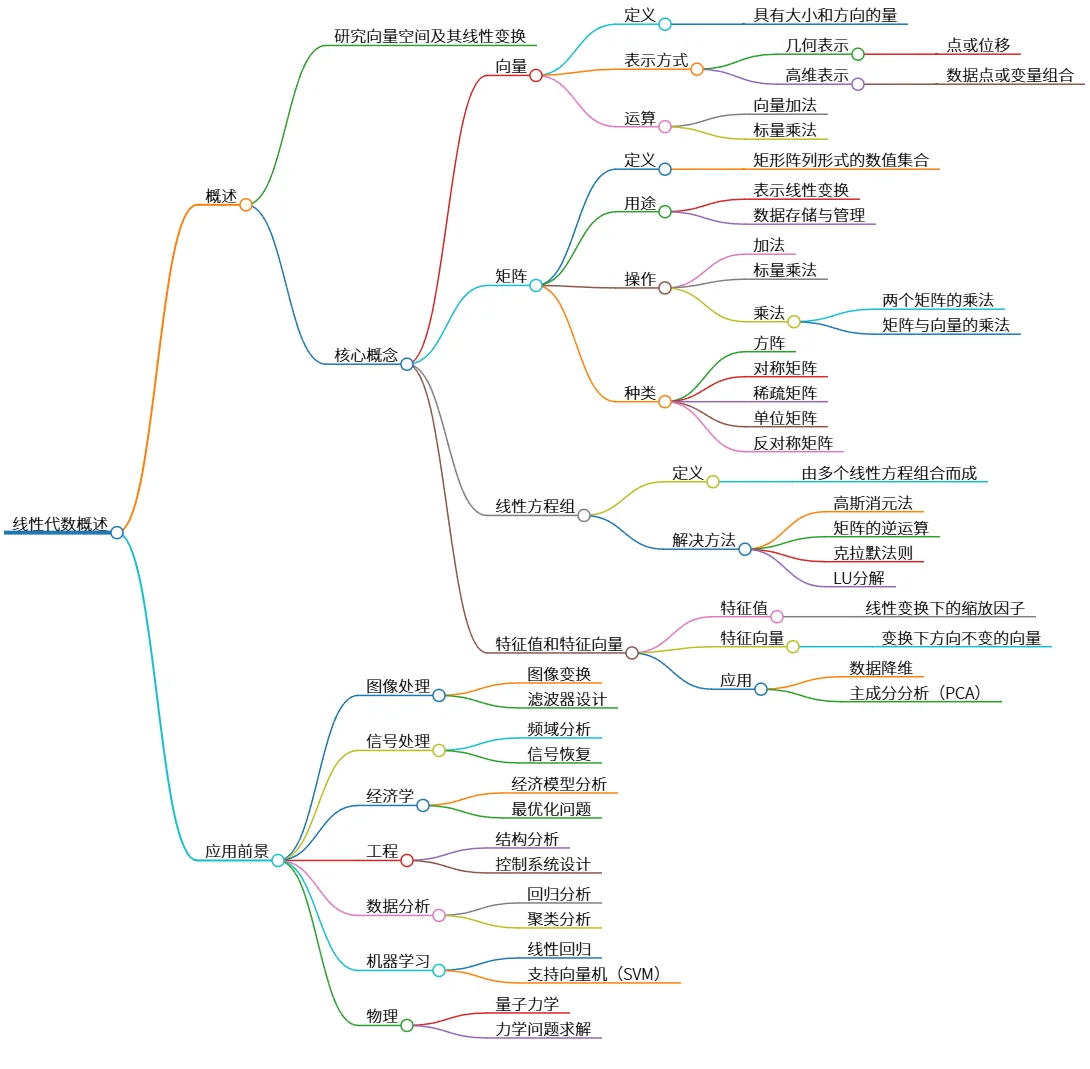
线性代数概述：向量、矩阵及其应用前景分析

该思维导图概述了线性代数的核心概念，包括向量、矩阵、线性方程组以及特征值和特征向量。向量是具有大小和方向的基本单元，矩阵则是处理线性变换的重要工具。线性方程组的解决方法包括高斯消元法和矩阵的逆运算。特征值和特征向量分别描述了线性变换的缩放因子和不变方向。线性代数在图像处理、信号处理、经济学、工程、数据分析、机器学习和物理等领域具有广泛的应用前景。

源码

# 线性代数概述
## 概述
- 研究向量空间及其线性变换
- 核心概念
  - 向量
    - 定义
      - 具有大小和方向的量
    - 表示方式
      - 几何表示
        - 点或位移
      - 高维表示
        - 数据点或变量组合
    - 运算
      - 向量加法
      - 标量乘法
  - 矩阵
    - 定义
      - 矩形阵列形式的数值集合
    - 用途
      - 表示线性变换
      - 数据存储与管理
    - 操作
      - 加法
      - 标量乘法
      - 乘法
        - 两个矩阵的乘法
        - 矩阵与向量的乘法
    - 种类
      - 方阵
      - 对称矩阵
      - 稀疏矩阵
      - 单位矩阵
      - 反对称矩阵
  - 线性方程组
    - 定义
      - 由多个线性方程组合而成
    - 解决方法
      - 高斯消元法
      - 矩阵的逆运算
      - 克拉默法则
      - LU分解
  - 特征值和特征向量
    - 特征值
      - 线性变换下的缩放因子
    - 特征向量
      - 变换下方向不变的向量
    - 应用
      - 数据降维
      - 主成分分析（PCA）
## 应用前景
- 图像处理
  - 图像变换
  - 滤波器设计
- 信号处理
  - 频域分析
  - 信号恢复
- 经济学
  - 经济模型分析
  - 最优化问题
- 工程
  - 结构分析
  - 控制系统设计
- 数据分析
  - 回归分析
  - 聚类分析
- 机器学习
  - 线性回归
  - 支持向量机（SVM）
- 物理
  - 量子力学
  - 力学问题求解

图片