向量代数与空间解析几何的基本概念与应用
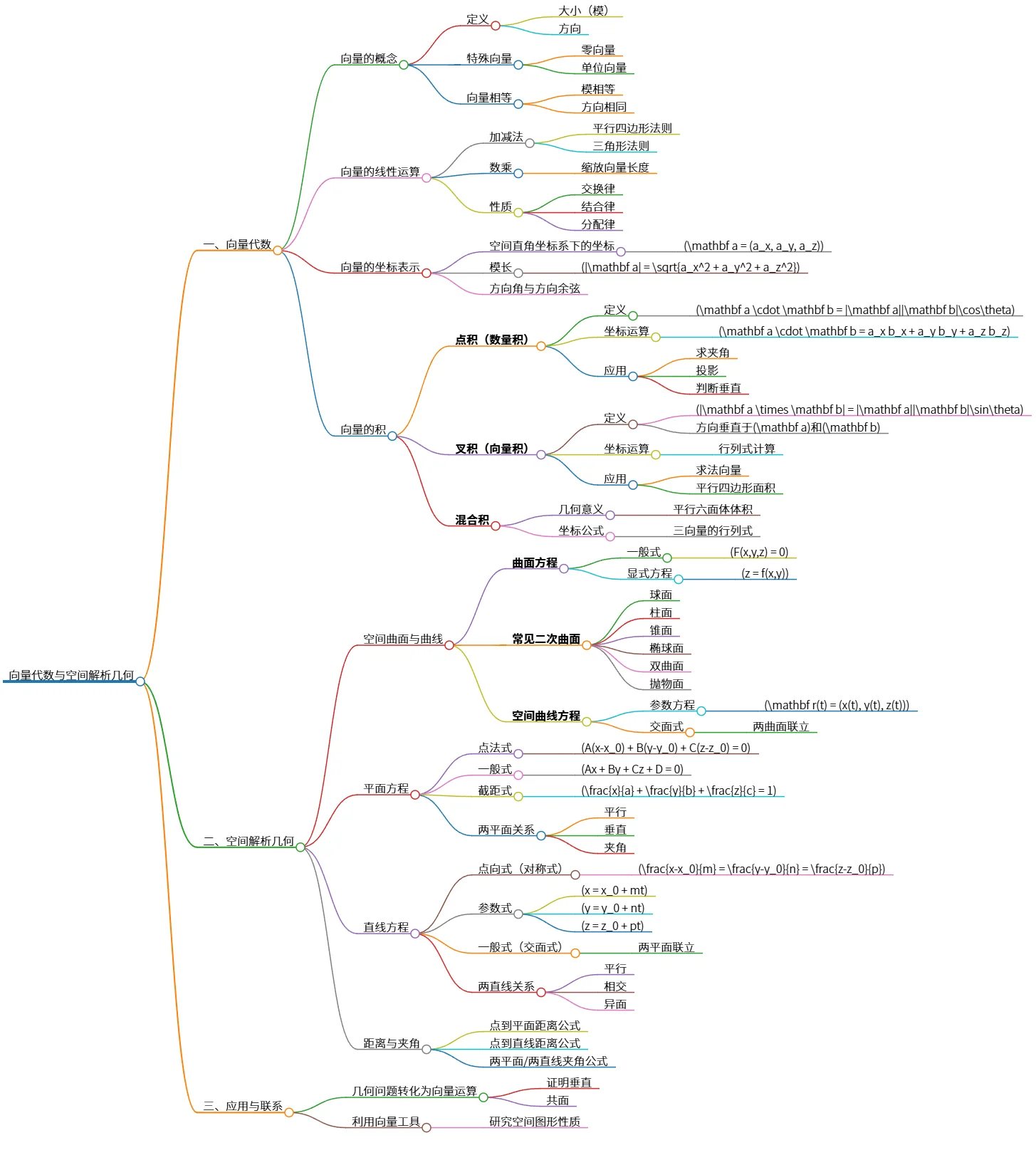
该思维导图概述了向量代数与空间解析几何的基本概念与运算。向量的定义、线性运算、坐标表示及其积(点积、叉积、混合积)被系统介绍,强调了几何应用。空间解析几何部分涵盖了曲面与曲线的方程、平面和直线的方程及其关系,此外,还探讨了距离与夹角的计算方法。最后,指出几何问题可通过向量运算进行转化与研究。
源码
# 向量代数与空间解析几何
## 一、向量代数
### 向量的概念
- 定义
- 大小(模)
- 方向
- 特殊向量
- 零向量
- 单位向量
- 向量相等
- 模相等
- 方向相同
### 向量的线性运算
- 加减法
- 平行四边形法则
- 三角形法则
- 数乘
- 缩放向量长度
- 性质
- 交换律
- 结合律
- 分配律
### 向量的坐标表示
- 空间直角坐标系下的坐标
- \(\mathbf a = (a_x, a_y, a_z)\)
- 模长
- \(|\mathbf a| = \sqrt{a_x^2 + a_y^2 + a_z^2}\)
- 方向角与方向余弦
### 向量的积
- **点积(数量积)**
- 定义
- \(\mathbf a \cdot \mathbf b = |\mathbf a||\mathbf b|\cos\theta\)
- 坐标运算
- \(\mathbf a \cdot \mathbf b = a_x b_x + a_y b_y + a_z b_z\)
- 应用
- 求夹角
- 投影
- 判断垂直
- **叉积(向量积)**
- 定义
- \(|\mathbf a \times \mathbf b| = |\mathbf a||\mathbf b|\sin\theta\)
- 方向垂直于\(\mathbf a\)和\(\mathbf b\)
- 坐标运算
- 行列式计算
- 应用
- 求法向量
- 平行四边形面积
- **混合积**
- 几何意义
- 平行六面体体积
- 坐标公式
- 三向量的行列式
## 二、空间解析几何
### 空间曲面与曲线
- **曲面方程**
- 一般式
- \(F(x,y,z) = 0\)
- 显式方程
- \(z = f(x,y)\)
- **常见二次曲面**
- 球面
- 柱面
- 锥面
- 椭球面
- 双曲面
- 抛物面
- **空间曲线方程**
- 参数方程
- \(\mathbf r(t) = (x(t), y(t), z(t))\)
- 交面式
- 两曲面联立
### 平面方程
- 点法式
- \(A(x-x_0) + B(y-y_0) + C(z-z_0) = 0\)
- 一般式
- \(Ax + By + Cz + D = 0\)
- 截距式
- \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\)
- 两平面关系
- 平行
- 垂直
- 夹角
### 直线方程
- 点向式(对称式)
- \(\frac{x-x_0}{m} = \frac{y-y_0}{n} = \frac{z-z_0}{p}\)
- 参数式
- \(x = x_0 + mt\)
- \(y = y_0 + nt\)
- \(z = z_0 + pt\)
- 一般式(交面式)
- 两平面联立
- 两直线关系
- 平行
- 相交
- 异面
### 距离与夹角
- 点到平面距离公式
- 点到直线距离公式
- 两平面/两直线夹角公式
## 三、应用与联系
- 几何问题转化为向量运算
- 证明垂直
- 共面
- 利用向量工具
- 研究空间图形性质
图片