复数与复变函数的基础知识与运算法则详解
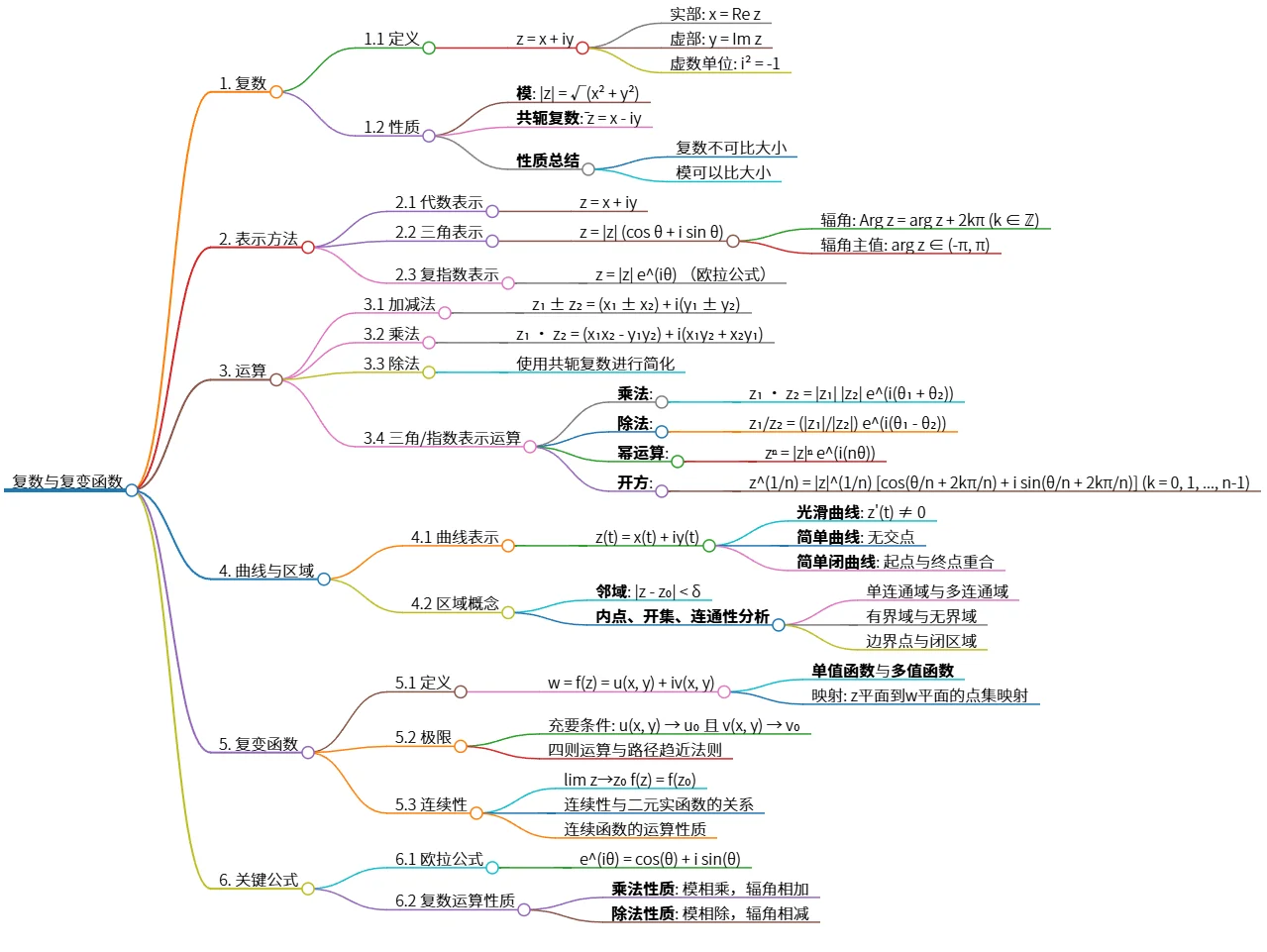
该思维导图概述了复数和复变函数的基本概念,包括复数的定义及其性质、表示方法(代数、三角、复指数)、运算规则(加减、乘法、除法、幂运算等)、曲线与区域的概念、复变函数的定义与连续性等。关键公式如欧拉公式以及复数运算的性质也被提及,为理解复数的性质与应用提供了系统性框架。
源码
# 复数与复变函数
## 1. 复数
### 1.1 定义
- z = x + iy
- 实部: x = Re z
- 虚部: y = Im z
- 虚数单位: i² = -1
### 1.2 性质
- **模**: |z| = √(x² + y²)
- **共轭复数**: ̄z = x - iy
- **性质总结**
- 复数不可比大小
- 模可以比大小
## 2. 表示方法
### 2.1 代数表示
- z = x + iy
### 2.2 三角表示
- z = |z| (cos θ + i sin θ)
- 辐角: Arg z = arg z + 2kπ (k ∈ ℤ)
- 辐角主值: arg z ∈ (-π, π)
### 2.3 复指数表示
- z = |z| e^(iθ) (欧拉公式)
## 3. 运算
### 3.1 加减法
- z₁ ± z₂ = (x₁ ± x₂) + i(y₁ ± y₂)
### 3.2 乘法
- z₁ · z₂ = (x₁x₂ - y₁y₂) + i(x₁y₂ + x₂y₁)
### 3.3 除法
- 使用共轭复数进行简化
### 3.4 三角/指数表示运算
- **乘法**:
- z₁ · z₂ = |z₁| |z₂| e^(i(θ₁ + θ₂))
- **除法**:
- z₁/z₂ = (|z₁|/|z₂|) e^(i(θ₁ - θ₂))
- **幂运算**:
- zⁿ = |z|ⁿ e^(i(nθ))
- **开方**:
- z^(1/n) = |z|^(1/n) [cos(θ/n + 2kπ/n) + i sin(θ/n + 2kπ/n)] (k = 0, 1, ..., n-1)
## 4. 曲线与区域
### 4.1 曲线表示
- z(t) = x(t) + iy(t)
- **光滑曲线**: z'(t) ≠ 0
- **简单曲线**: 无交点
- **简单闭曲线**: 起点与终点重合
### 4.2 区域概念
- **邻域**: |z - z₀| < δ
- **内点、开集、连通性分析**
- 单连通域与多连通域
- 有界域与无界域
- 边界点与闭区域
## 5. 复变函数
### 5.1 定义
- w = f(z) = u(x, y) + iv(x, y)
- **单值函数**与**多值函数**
- 映射: z平面到w平面的点集映射
### 5.2 极限
- 充要条件: u(x, y) → u₀ 且 v(x, y) → v₀
- 四则运算与路径趋近法则
### 5.3 连续性
- lim z→z₀ f(z) = f(z₀)
- 连续性与二元实函数的关系
- 连续函数的运算性质
## 6. 关键公式
### 6.1 欧拉公式
- e^(iθ) = cos(θ) + i sin(θ)
### 6.2 复数运算性质
- **乘法性质**: 模相乘,辐角相加
- **除法性质**: 模相除,辐角相减
图片