生物统计学方差分析的基本原理与应用技巧

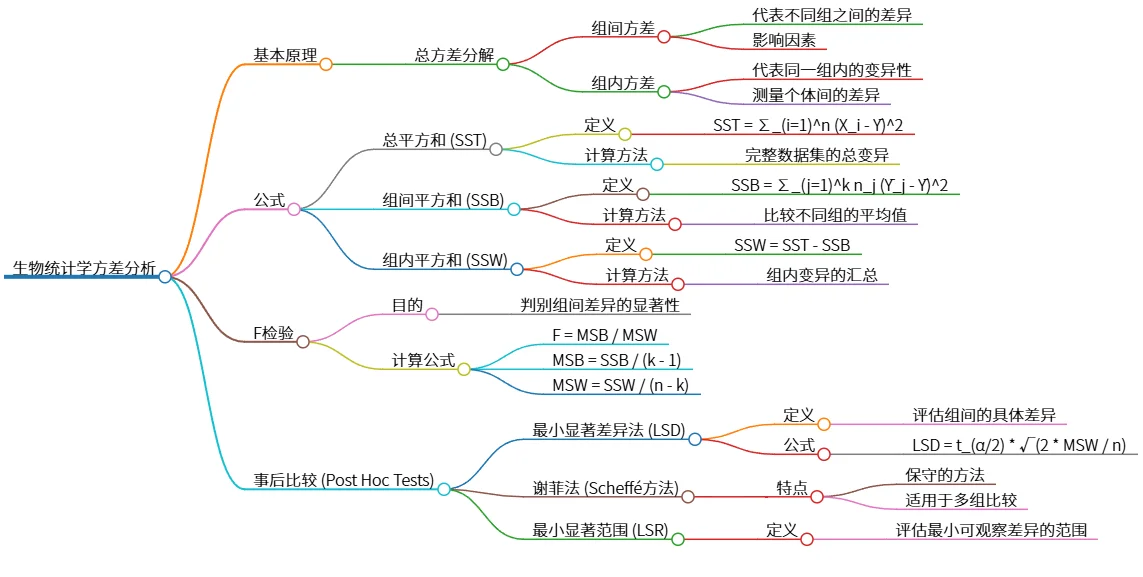
该思维导图概述了生物统计学中方差分析的基本原理，包括总方差的分解为组间方差和组内方差。提供了重要的公式，如总平方和（SST）、组间平方和（SSB）和组内平方和（SSW），以及F检验的计算方法。还提到了事后比较方法，例如最小显著差异法（LSD）、谢菲法和最小显著范围（LSR），用于评估组间差异的显著性。

源码

# 生物统计学方差分析
## 基本原理
- 总方差分解
  - 组间方差
    - 代表不同组之间的差异
    - 影响因素
  - 组内方差
    - 代表同一组内的变异性
    - 测量个体间的差异
## 公式
- 总平方和 (SST)
  - 定义
    - SST = ∑_(i=1)^n (X_i - Ȳ)^2
  - 计算方法
    - 完整数据集的总变异
- 组间平方和 (SSB)
  - 定义
    - SSB = ∑_(j=1)^k n_j (Ȳ_j - Ȳ)^2
  - 计算方法
    - 比较不同组的平均值
- 组内平方和 (SSW)
  - 定义
    - SSW = SST - SSB
  - 计算方法
    - 组内变异的汇总
## F检验
- 目的
  - 判别组间差异的显著性
- 计算公式
  - F = MSB / MSW
  - MSB = SSB / (k - 1)
  - MSW = SSW / (n - k)
## 事后比较 (Post Hoc Tests)
- 最小显著差异法 (LSD)
  - 定义
    - 评估组间的具体差异
  - 公式
    - LSD = t_(α/2) * √(2 * MSW / n)
- 谢菲法 (Scheffé方法)
  - 特点
    - 保守的方法
    - 适用于多组比较
- 最小显著范围 (LSR)
  - 定义
    - 评估最小可观察差异的范围

图片