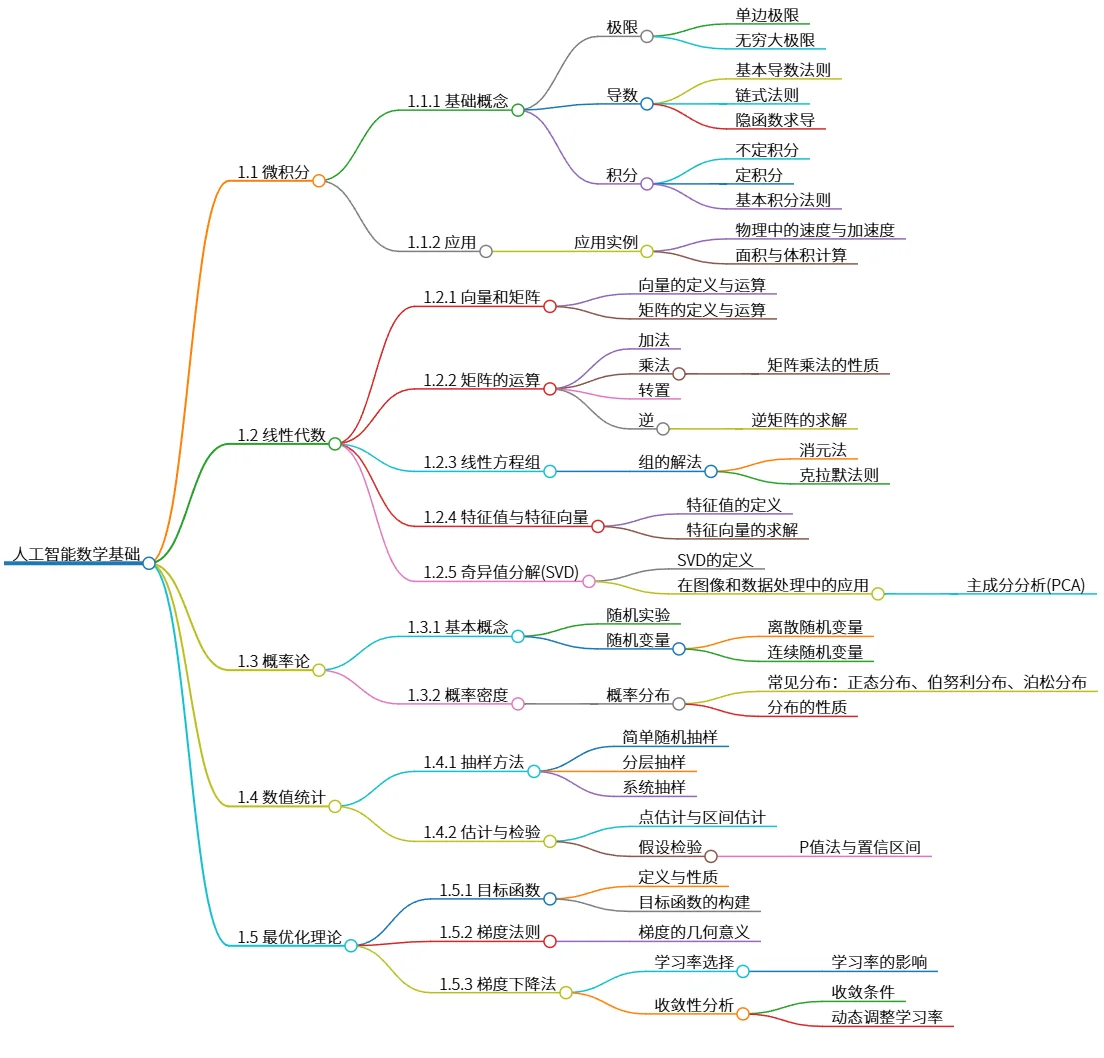
人工智能数学基础：微积分、线性代数与概率统计

该思维导图概述了人工智能相关的数学基础知识，涵盖微积分（极限、导数、积分）、线性代数（向量、矩阵运算、线性方程组、特征值、特征向量、奇异值分解及其应用）、概率论（随机变量、概率密度）以及数值统计（抽样方法、估计与检验）、最优化理论（目标函数、梯度法则、梯度下降法及其学习率选择与收敛性分析）。这些数学分支是理解和构建人工智能算法的关键，特别是深度学习模型的训练和优化。

源码

# 人工智能数学基础
## 1.1 微积分
### 1.1.1 基础概念
- 极限
  - 单边极限
  - 无穷大极限
- 导数
  - 基本导数法则
  - 链式法则
  - 隐函数求导
- 积分
  - 不定积分
  - 定积分
  - 基本积分法则
### 1.1.2 应用
- 应用实例
  - 物理中的速度与加速度
  - 面积与体积计算

## 1.2 线性代数
### 1.2.1 向量和矩阵
- 向量的定义与运算
- 矩阵的定义与运算
### 1.2.2 矩阵的运算
- 加法
- 乘法
  - 矩阵乘法的性质
- 转置
- 逆
  - 逆矩阵的求解
### 1.2.3 线性方程组
- 组的解法
  - 消元法
  - 克拉默法则
### 1.2.4 特征值与特征向量
- 特征值的定义
- 特征向量的求解
### 1.2.5 奇异值分解(SVD)
- SVD的定义
- 在图像和数据处理中的应用
  - 主成分分析(PCA)

## 1.3 概率论
### 1.3.1 基本概念
- 随机实验
- 随机变量
  - 离散随机变量
  - 连续随机变量
### 1.3.2 概率密度
- 概率分布
  - 常见分布：正态分布、伯努利分布、泊松分布
  - 分布的性质

## 1.4 数值统计
### 1.4.1 抽样方法
- 简单随机抽样
- 分层抽样
- 系统抽样
### 1.4.2 估计与检验
- 点估计与区间估计
- 假设检验
  - P值法与置信区间

## 1.5 最优化理论
### 1.5.1 目标函数
- 定义与性质
- 目标函数的构建
### 1.5.2 梯度法则
- 梯度的几何意义
### 1.5.3 梯度下降法
- 学习率选择
  - 学习率的影响
- 收敛性分析
  - 收敛条件
  - 动态调整学习率

图片