概率论基础:随机变量、概率分布及应用
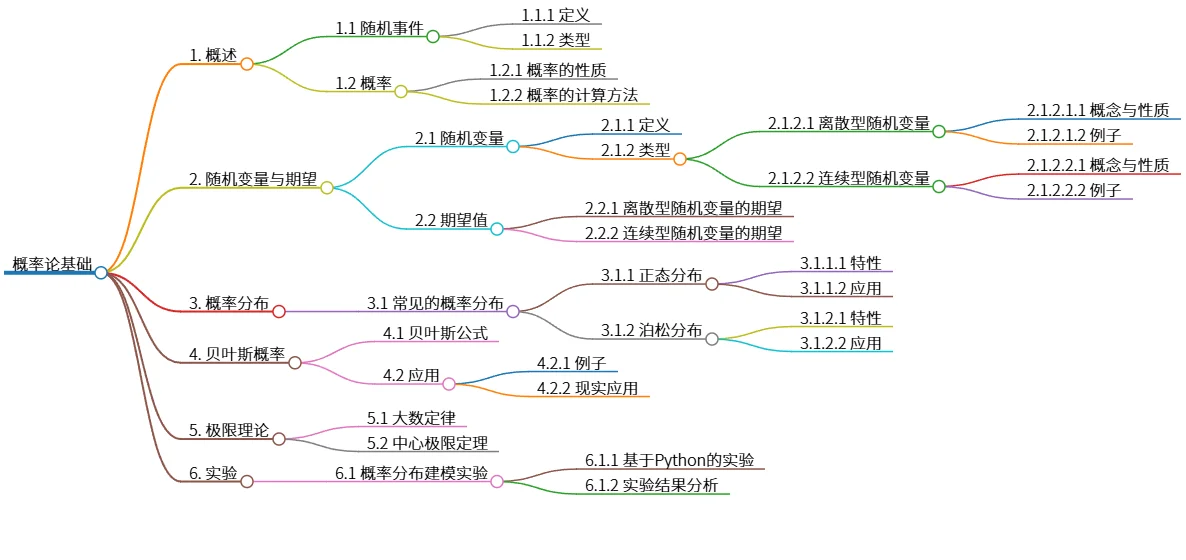
该思维导图概述了概率论的核心内容,包括随机事件与概率、随机变量及其期望值(离散型与连续型),常见的概率分布(正态分布、泊松分布),以及贝叶斯概率(贝叶斯公式及应用)。此外,还涵盖了概率论中的极限理论,例如大数定律和中心极限定理,并提及了基于Python进行概率分布建模的实验。 总而言之,该导图系统地展现了概率论的基本概念、核心方法和应用案例。
源码
# 概率论基础
## 1. 概述
### 1.1 随机事件
#### 1.1.1 定义
#### 1.1.2 类型
### 1.2 概率
#### 1.2.1 概率的性质
#### 1.2.2 概率的计算方法
## 2. 随机变量与期望
### 2.1 随机变量
#### 2.1.1 定义
#### 2.1.2 类型
##### 2.1.2.1 离散型随机变量
###### 2.1.2.1.1 概念与性质
###### 2.1.2.1.2 例子
##### 2.1.2.2 连续型随机变量
###### 2.1.2.2.1 概念与性质
###### 2.1.2.2.2 例子
### 2.2 期望值
#### 2.2.1 离散型随机变量的期望
#### 2.2.2 连续型随机变量的期望
## 3. 概率分布
### 3.1 常见的概率分布
#### 3.1.1 正态分布
##### 3.1.1.1 特性
##### 3.1.1.2 应用
#### 3.1.2 泊松分布
##### 3.1.2.1 特性
##### 3.1.2.2 应用
## 4. 贝叶斯概率
### 4.1 贝叶斯公式
### 4.2 应用
#### 4.2.1 例子
#### 4.2.2 现实应用
## 5. 极限理论
### 5.1 大数定律
### 5.2 中心极限定理
## 6. 实验
### 6.1 概率分布建模实验
#### 6.1.1 基于Python的实验
#### 6.1.2 实验结果分析
图片