相反数：数轴上的对称与0的特殊性

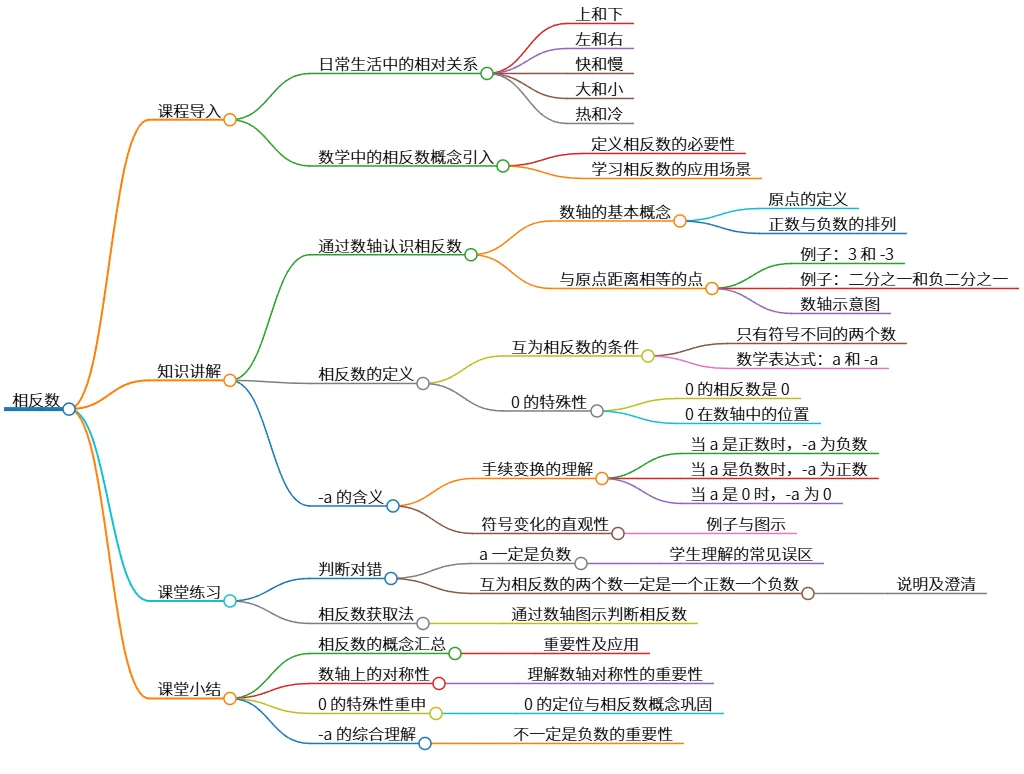
该思维导图总结了相反数的概念和相关知识。首先从日常生活中的相对关系引入相反数的概念，然后通过数轴直观地解释了相反数：与原点距离相等，符号相反。定义中明确指出只有符号不同的两个数互为相反数，0 的相反数是 0，并详细解释了“-a”的含义，它取决于 a 的正负。最后通过课堂练习巩固了对相反数概念的理解，并强调了“-a”不一定是负数这一重要结论。整个思维导图条理清晰，循序渐进。

源码

# 相反数
## 课程导入
- 日常生活中的相对关系
  - 上和下
  - 左和右
  - 快和慢
  - 大和小
  - 热和冷
- 数学中的相反数概念引入
  - 定义相反数的必要性
  - 学习相反数的应用场景

## 知识讲解
### 通过数轴认识相反数
- 数轴的基本概念
  - 原点的定义
  - 正数与负数的排列
- 与原点距离相等的点
  - 例子：3 和 -3
  - 例子：二分之一和负二分之一
  - 数轴示意图

### 相反数的定义
- 互为相反数的条件
  - 只有符号不同的两个数
  - 数学表达式：a 和 -a
- 0 的特殊性
  - 0 的相反数是 0
  - 0 在数轴中的位置

### -a 的含义
- 手续变换的理解
  - 当 a 是正数时，-a 为负数
  - 当 a 是负数时，-a 为正数
  - 当 a 是 0 时，-a 为 0
- 符号变化的直观性
  - 例子与图示

## 课堂练习
- 判断对错
  - a 一定是负数
    - 学生理解的常见误区
  - 互为相反数的两个数一定是一个正数一个负数
    - 说明及澄清
- 相反数获取法
  - 通过数轴图示判断相反数

## 课堂小结
- 相反数的概念汇总
  - 重要性及应用
- 数轴上的对称性
  - 理解数轴对称性的重要性
- 0 的特殊性重申
  - 0 的定位与相反数概念巩固
- -a 的综合理解
  - 不一定是负数的重要性

图片