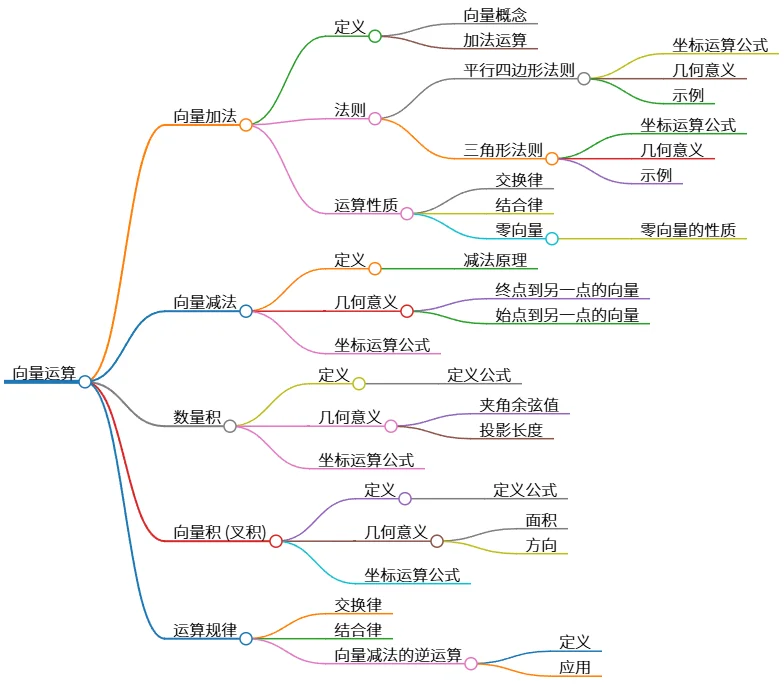
向量运算:加法、减法、数量积与向量积
该思维导图总结了向量运算的常用知识点,包括向量加法(平行四边形法则和三角形法则,包含坐标运算公式及几何意义,并阐述了交换律、结合律和零向量的性质)、向量减法(定义、几何意义及坐标运算公式)、数量积(定义、几何意义、坐标运算公式)、向量积(叉积,包含定义、几何意义及坐标运算公式),以及向量运算的整体规律(交换律、结合律和向量减法的逆运算)。 它系统地梳理了向量运算的基本概念、运算方法和几何解释。
源码
# 向量运算
## 向量加法
### 定义
#### 向量概念
#### 加法运算
### 法则
#### 平行四边形法则
##### 坐标运算公式
##### 几何意义
##### 示例
#### 三角形法则
##### 坐标运算公式
##### 几何意义
##### 示例
### 运算性质
#### 交换律
#### 结合律
#### 零向量
##### 零向量的性质
## 向量减法
### 定义
#### 减法原理
### 几何意义
#### 终点到另一点的向量
#### 始点到另一点的向量
### 坐标运算公式
## 数量积
### 定义
#### 定义公式
### 几何意义
#### 夹角余弦值
#### 投影长度
### 坐标运算公式
## 向量积 (叉积)
### 定义
#### 定义公式
### 几何意义
#### 面积
#### 方向
### 坐标运算公式
## 运算规律
### 交换律
### 结合律
### 向量减法的逆运算
#### 定义
#### 应用
图片